Complex Numbers
Welcome to Our Site
I greet you this day,
For the Classic ACT exam:
The ACT Mathematics test is a timed exam...60 questions in 60 minutes
This implies that you have to solve each question in one minute.
Each of the first 20 questions (less challenging) will typically take less than a minute a solve.
Each of the next 20 questions (medium challenging) may take about a minute to solve.
Each of the last 20 questions (more challenging) may take more than a minute to solve.
The goal is to maximize your time.
You use the time saved on the questions you solve in less than a minute to solve questions that will take more
than a minute.
So, you should try to solve each question correctly and timely.
So, it is not just solving a question correctly, but solving it correctly on time.
Please ensure you attempt all ACT questions.
There is no negative penalty for a wrong answer.
Also: please note that unless specified otherwise, geometric figures are drawn to scale. So, you can figure out
the correct answer by eliminating the incorrect options.
Other suggestions are listed in the solutions/explanations as applicable.
These are the solutions to the ACT past questions on the topics: Complex Numbers.
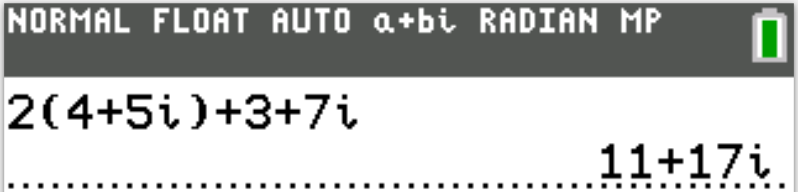
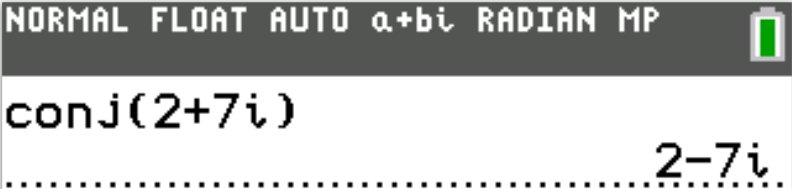
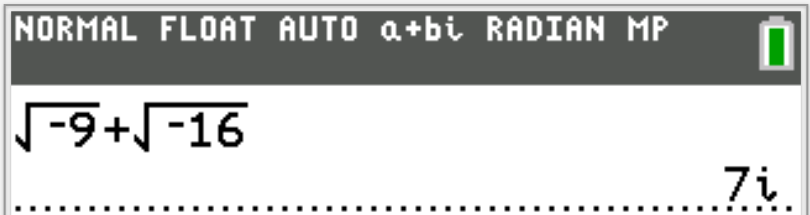
When applicable, the TI-84 Plus CE calculator (also applicable to TI-84 Plus calculator) solutions are provided
for some questions.
The link to the video solutions will be provided for you. Please
subscribe to the YouTube channel to be notified of upcoming livestreams. You are welcome to ask questions during
the video livestreams.
If you find these resources valuable and helpful in your passing the
Mathematics test of the ACT, please consider making a donation:
Cash App: $ExamsSuccess or
cash.app/ExamsSuccess
PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess
Google charges me for the hosting of this website and my other
educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well.
As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.
Comments, ideas, areas of improvement, questions, and constructive
criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.
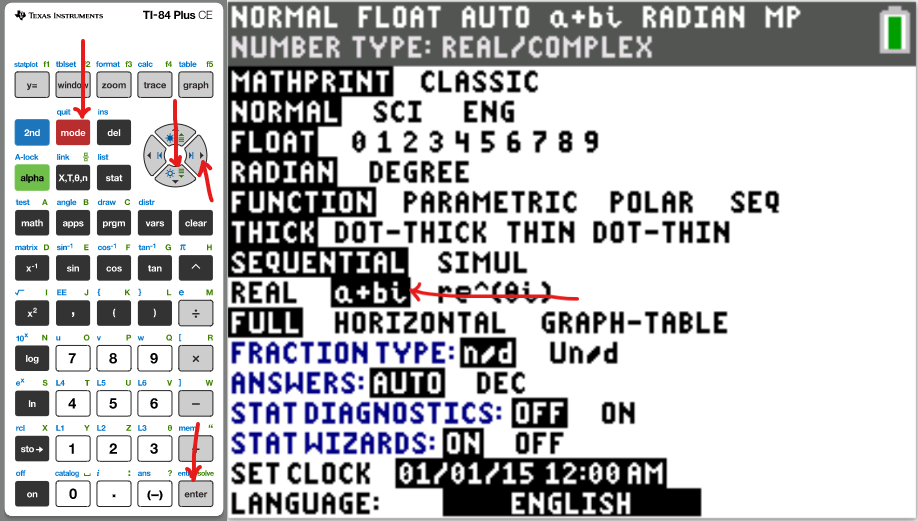
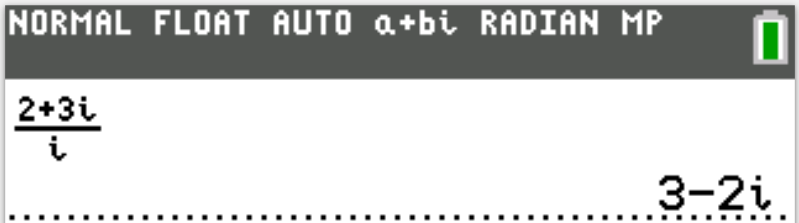
Please NOTE: For applicable questions, if you intend to use the TI-84 Family:
Please make sure you set the MODE to $\boldsymbol{a + bi}$ (Complex Number mode).
It is REAL by default. So, it needs to be set to $\boldsymbol{a + bi}$.
What is the value of $2z + w$?
$ F.\;\; -28 \\[3ex] G.\;\; 28i \\[3ex] H.\;\; 11 + 12i \\[3ex] J.\;\; 11 + 17i \\[3ex] K.\;\; 14 + 24i \\[3ex] $
$ z = 4 + 5i \\[3ex] w = 3 + 7i \\[3ex] 2z + w \\[3ex] = 2(4 + 5i) + (3 + 7i) \\[3ex] = 8 + 10i + 3 + 7i \\[3ex] = 11 + 17i $
$ A.\;\; -5 \\[3ex] B.\;\; 9 \\[3ex] C.\;\; 9i \\[3ex] D.\;\; \sqrt{53} \\[3ex] E.\;\; 2 - 7i \\[3ex] $
The complex conjugate of 2 + 7i is 2 − 7i
$ A.\;\; 7i \\[3ex] B.\;\; 5i \\[3ex] C.\;\; 7 \\[3ex] D.\;\; 5 \\[3ex] E.\;\; -5 \\[3ex] $
Sum is the result of an addition operation
$ \sqrt{-9} + \sqrt{-16} \\[3ex] 3i + 4i \\[3ex] 7i $
$ A.\;\; 7 \\[3ex] B.\;\; 25 \\[3ex] C.\;\; 7 + 24i \\[3ex] D.\;\; 8 + 6i \\[3ex] E.\;\; 25 + 24i \\[3ex] $
$ i = \sqrt{-1} \\[3ex] i^2 = -1 \\[5ex] (4 + 3i)^2 \\[4ex] (4 + 3i)(4 + 3i) \\[3ex] 16 + 12i + 12i + 9i^2 \\[3ex] 16 + 24i + 9(-1) \\[3ex] 16 + 24i + -9 \\[3ex] 16 + 24i - 9 \\[3ex] 7 + 24i $
