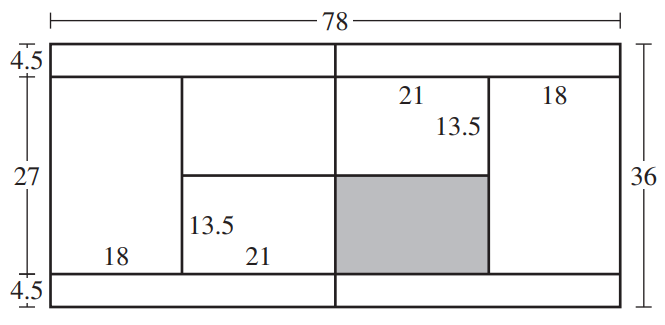
Mensuration
Welcome to Our Site
I greet you this day,
For the Classic ACT exam:
The ACT Mathematics test is a timed exam...60 questions in 60 minutes
This implies that you have to solve each question in one minute.
Each of the first 20 questions (less challenging) will typically take less than a minute a solve.
Each of the next 20 questions (medium challenging) may take about a minute to solve.
Each of the last 20 questions (more challenging) may take more than a minute to solve.
The goal is to maximize your time.
You use the time saved on the questions you solve in less than a minute to solve questions that will take more
than a minute.
So, you should try to solve each question correctly and timely.
So, it is not just solving a question correctly, but solving it correctly on time.
Please ensure you attempt all ACT questions.
There is no negative penalty for a wrong answer.
Also: please note that unless specified otherwise, geometric figures are drawn to scale. So, you can figure out
the correct answer by eliminating the incorrect options.
Other suggestions are listed in the solutions/explanations as applicable.
These are the solutions to the ACT past questions on the topics in Mensuration.
When applicable, the TI-84 Plus CE calculator (also applicable to TI-84 Plus calculator) solutions are provided
for some questions.
The link to the video solutions will be provided for you. Please
subscribe to the YouTube channel to be notified of upcoming livestreams. You are welcome to ask questions during
the video livestreams.
If you find these resources valuable and if any of these resources were helpful in your passing the
Mathematics test of the ACT, please consider making a donation:
Cash App: $ExamsSuccess or
cash.app/ExamsSuccess
PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess
Google charges me for the hosting of this website and my other
educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well.
As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.
Comments, ideas, areas of improvement, questions, and constructive
criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.
Formulas
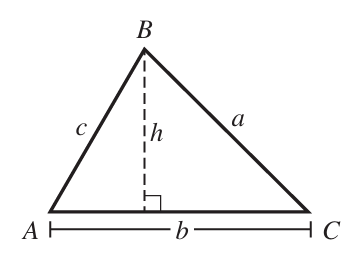
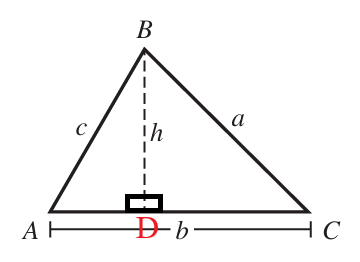
Right Triangle
$ perpendicular\:\:height = height \\[3ex] Area = \dfrac{1}{2} * base * height \\[5ex] height = \dfrac{2 * Area}{base} \\[5ex] base = \dfrac{2 * Area}{height} \\[5ex] hypotenuse^2 = height^2 + base^2...Pythagorean\:\:Theorem \\[3ex] hypotenuse = \sqrt{height^2 + base^2} \\[3ex] height = \sqrt{hypotenuse^2 - base^2} \\[3ex] base = \sqrt{hypotenuse^2 - height^2} \\[3ex] Perimeter = hypotenuse + height + base \\[3ex] Area = \dfrac{1}{2} * height * base * \sin (hypotenuseAngle) \\[5ex] Area = \dfrac{1}{2} * height * hypotenuse * \sin (baseAngle) \\[5ex] Area = \dfrac{1}{2} * base * hypotenuse * \sin (heightAngle) \\[5ex] Semiperimeter = \dfrac{height + base + hypotenuse}{2} \\[5ex] Semiperimeter - height = firstdifference \\[3ex] Semiperimeter - base = seconddifference \\[3ex] Semiperimeter - hypotenuse = thirddifference \\[3ex] Area = \sqrt{Semiperimeter * firstdifference * seconddifference * thirddifference}...Hero's\:\:Formula\:\:or\:\:Heron's\:\:Formula \\[5ex] hypotenuse = {Perimeter^2 - 4 * Area}{2 * Perimeter} \\[5ex] base = \dfrac{(Perimeter - hypotenuse) \pm Math.sqrt((hypotenuse - Perimeter)^2 - 8 * Area)}{2} \\[5ex] height = \dfrac{2 * Area}{base} $
Triangle
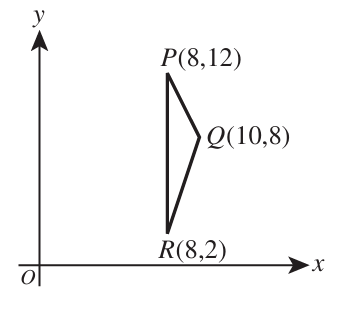
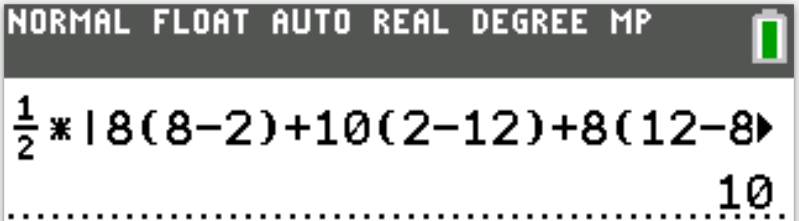
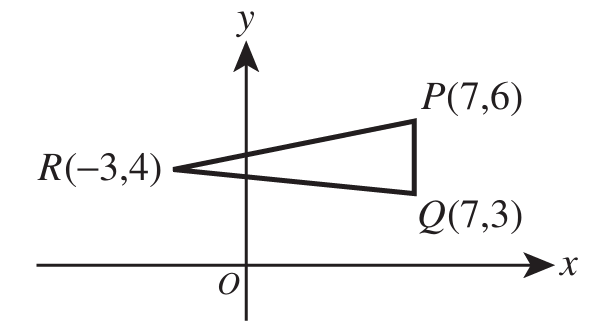
$ Perimeter = firstside + secondside + thirdside \\[5ex] Area = \dfrac{1}{2} * firstside * secondside * \sin (thirdAngle) \\[5ex] Area = \dfrac{1}{2} * firstside * thirdside * \sin (secondAngle) \\[5ex] Area = \dfrac{1}{2} * secondside * thirdside * \sin (firstAngle) \\[5ex] Semiperimeter = \dfrac{firstside + secondside + thirdside}{2} \\[5ex] Semiperimeter - firstside = firstdifference \\[3ex] Semiperimeter - secondside = seconddifference \\[3ex] Semiperimeter - thirdside = thirddifference \\[3ex] Area = \sqrt{Semiperimeter * firstdifference * seconddifference * thirddifference}...Hero's\:\:Formula\:\:or\:\:Heron's\:\:Formula \\[5ex] \underline{Cosine\:\:Law} \\[3ex] firstside^2 = secondside^2 + thirdside^2 - 2 * secondside * thirdside * \cos (firstAngle) \\[3ex] secondside^2 = firstside^2 + thirdside^2 - 2 * firstside * thirdside * \cos (secondAngle) \\[3ex] thirdside^2 = firstside^2 + secondside^2 - 2 * firstside * secondside * \cos (thirdAngle) \\[5ex] firstAngle = \cos^{-1} \left(\dfrac{secondside^2 + thirdside^2 - firstside^2}{2 * secondside * thirdside}\right) \\[5ex] secondAngle = \cos^{-1} \left(\dfrac{firstside^2 + thirdside^2 - secondside^2}{2 * firstside * thirdside}\right) \\[5ex] thirdAngle = \cos^{-1} \left(\dfrac{firstside^2 + secondside^2 - thirdside^2}{2 * firstside * secondside}\right) \\[7ex] \underline{\text{Area of a Triangle given the vertices}} \\[3ex] \text{Let the vertices be:} \\[3ex] Vertex\;1:\;\;(x_1, y_1) \\[4ex] Vertex\;2:\;\;(x_2, y_2) \\[4ex] Vertex\;3:\;\;(x_3, y_3) \\[4ex] Area = \dfrac{1}{2}|x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| $
Insribed Triangle (Circumscribed Circle)
$ Circumradius = \dfrac{firstside \cdot secondside \cdot thirdside}{4 \cdot Area} $
Square
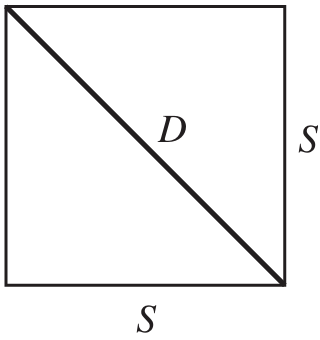
$ side = length = width = height \\[3ex] Area = side^2 \\[3ex] side = \sqrt{Area} \\[3ex] Perimeter = 4 * side \\[3ex] side = \dfrac{Perimeter}{4} \\[5ex] diagonal = side * \sqrt{2} \\[3ex] side = \dfrac{diagonal * \sqrt{2}}{2} \\[5ex] Area = \dfrac{Perimeter^2}{16} \\[5ex] Perimeter = 4 * \sqrt{Area} \\[3ex] Area = \dfrac{diagonal^2}{2} \\[5ex] diagonal = \sqrt{2 * Area} \\[3ex] Perimeter = 2 * diagonal * \sqrt{2} \\[3ex] diagonal = \dfrac{Perimeter * \sqrt{2}}{4} $
Rectangle
$ Area = length * width \\[3ex] length = \dfrac{Area}{width} \\[5ex] width = \dfrac{Area}{length} \\[5ex] Area = \dfrac{(length * Perimeter) - (2 * length^2)}{2} \\[5ex] Area = \dfrac{(width * Perimeter) - (2 * width^2)}{2} \\[5ex] Perimeter = 2(length + width) \\[3ex] length = \dfrac{Perimeter - 2 * width}{2} \\[5ex] width = \dfrac{Perimeter - 2 * length}{2} \\[5ex] Perimeter = \dfrac{2(length^2 + Area)}{length} \\[5ex] Perimeter = \dfrac{2(width^2 + Area)}{width} \\[5ex] diagonal = \sqrt{length^2 + width^2} \\[4ex] length = \sqrt{diagonal^2 - width^2} \\[4ex] width = \sqrt{diagonal^2 - length^2} \\[4ex] diagonal = \dfrac{\sqrt{length^4 + Area^2}}{length} \\[5ex] diagonal = \dfrac{\sqrt{width^4 + Area^2}}{width} \\[5ex] diagonal = \dfrac{\sqrt{(Perimeter^2) + (5 * length^2) - (4 * Perimeter * length)}}{2} \\[5ex] diagonal = \dfrac{\sqrt{(Perimeter^2) + (5 * width^2) - (4 * Perimeter * width)}}{2} $
Circle
$ Area = A \\[3ex] Circumference = C \\[3ex] Radius = r \\[3ex] Diameter = d \\[3ex] d = 2r \\[3ex] r = \dfrac{d}{2} \\[5ex] A = \pi r^2 \\[3ex] A = \dfrac{\pi d^2}{4} \\[5ex] C = 2\pi r \\[3ex] C = \pi d \\[3ex] r = \dfrac{\sqrt{A\pi}}{\pi} \\[5ex] r = \dfrac{C}{2\pi} \\[5ex] d = \dfrac{2\sqrt{A\pi}}{\pi} \\[5ex] r = \dfrac{C}{\pi} \\[5ex] A = \dfrac{C^2}{4\pi} \\[5ex] C = 2\sqrt{A\pi} $
Cube
6 square faces
12 edges
$
edge = side = length = width = height \\[3ex]
Surface\:\:Area = 6 * edge^2 \\[3ex]
edge = \sqrt{\dfrac{Surface\:\:Area}{6}} \\[5ex]
Volume = edge^3 \\[3ex]
edge = \sqrt[3]{Volume} \\[3ex]
Volume = \dfrac{edge * Surface\:\: Area}{6} \\[5ex]
edge = \dfrac{6 * Volume}{Surface\:\:Area} \\[5ex]
Surface\:\:Area = \dfrac{6 * Volume}{edge} \\[5ex]
Volume = \dfrac{Surface\:\:Area * \sqrt{6 * Surface\:\:Area}}{36} \\[5ex]
edge = \dfrac{diagonal * \sqrt{3}}{3} \\[5ex]
diagonal = \sqrt{3} * edge \\[3ex]
Surface\:\:Area = 2 * diagonal^2 \\[3ex]
diagonal = \dfrac{\sqrt{2 * Surface\:\:Area}}{2} \\[5ex]
Volume = \dfrac{diagonal^3 * \sqrt{3}}{9} \\[5ex]
diagonal = \sqrt{3} * \sqrt[3]{Volume}
$
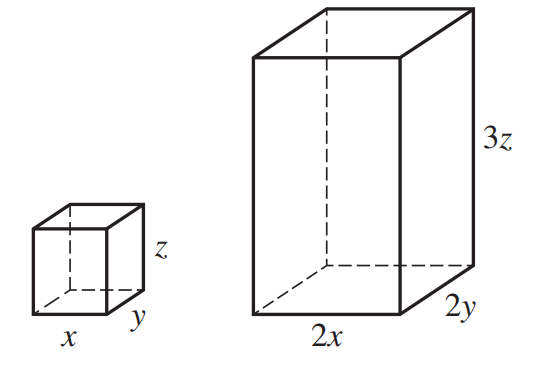
Cuboid (Right Rectangular Prism)
$ Volume = Length \cdot Width \cdot Height \\[3ex] $
Right Cone
Curved Surface Area = Lateral Surface Area
Height = Perpendicular Height
$
Volume\:\:of\:\:Cone = \dfrac{1}{3} * Volume\:\:of\:\:Cylinder \\[5ex]
Lateral\:\:Surface\:\:Area = LSA \\[3ex]
Base\:\:Area = BA \\[3ex]
Total\:\:Surface\:\:Area = TSA \\[3ex]
Volume = V \\[3ex]
Diameter = d \\[3ex]
Radius = r \\[3ex]
Height = h \\[3ex]
Slant Height = l \\[3ex]
r = \dfrac{d}{2} \\[5ex]
d = 2r \\[3ex]
l = \sqrt{h^2 + r^2} \\[3ex]
l = \dfrac{\sqrt{4h^2 + d^2}}{2} \\[5ex]
h = \sqrt{l^2 - r^2} \\[3ex]
h = \dfrac{\sqrt{4l^2 - d^2}}{2} \\[5ex]
r = \sqrt{l^2 - h^2} \\[3ex]
d = 2 * \sqrt{l^2 - h^2} \\[3ex]
BA = \pi r^2 \\[3ex]
r = \dfrac{\sqrt{BA * \pi}}{\pi} \\[5ex]
BA = \dfrac{\pi d^2}{4} \\[5ex]
d = \dfrac{2\sqrt{BA * \pi}}{\pi} \\[5ex]
LSA = \pi rl \\[3ex]
LSA = \dfrac{\pi dl}{2} \\[5ex]
l = \dfrac{LSA}{\pi r} \\[5ex]
LSA = \pi r\sqrt{h^2 + r^2} \\[3ex]
h = \dfrac{\sqrt{LSA^2 - \pi^2 r^4}}{\pi r} \\[5ex]
TSA = BA + LSA \\[3ex]
TSA = \pi r(r + l) \\[3ex]
l = \dfrac{TSA - \pi r^2}{\pi r} \\[5ex]
TSA = \dfrac{\pi d(d + 2l)}{4} \\[5ex]
l = \dfrac{4 * TSA - \pi d^2}{2\pi d} \\[5ex]
r = \dfrac{-\pi l \pm \sqrt{\pi^2 l^2 + 4\pi * TSA}}{2\pi} \\[5ex]
TSA = \pi r(r + \sqrt{h^2 + r^2}) \\[3ex]
h = \dfrac{\sqrt{TSA(TSA - 2\pi r^2)}}{\pi r} \\[5ex]
V = \dfrac{BA * h}{3} \\[5ex]
V = \dfrac{\pi r^2h}{3} \\[5ex]
V = \dfrac{\pi hd^2}{12} \\[5ex]
V = \dfrac{\pi h(l^2 - h^2)}{3} \\[5ex]
h = \dfrac{3V}{\pi r^2} \\[5ex]
r = \dfrac{\sqrt{3V\pi h}}{\pi h}
$
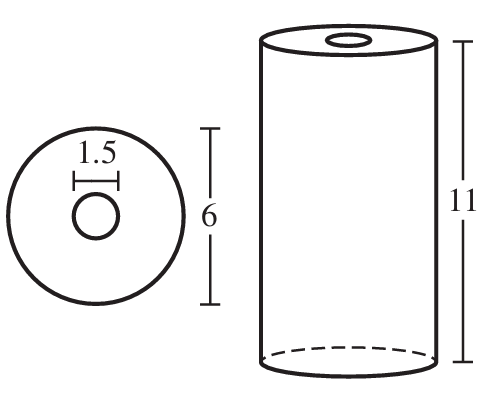
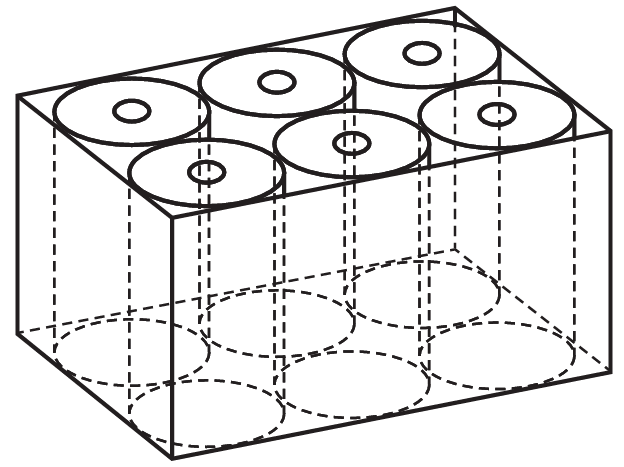
Right Cylinder
Curved Surface Area = Lateral Surface Area
Height = Perpendicular Height
$
Volume\:\:of\:\:Cylinder = 3 * Volume\:\:of\:\:Cone \\[3ex]
Lateral\:\:Surface\:\:Area = LSA \\[3ex]
Base\:\:Area = BA \\[3ex]
Total\:\:Surface\:\:Area = TSA \\[3ex]
Volume = V \\[3ex]
Diameter = d \\[3ex]
Radius = r \\[3ex]
Height = h \\[3ex]
r = \dfrac{d}{2} \\[5ex]
d = 2r \\[3ex]
LSA = 2\pi rh \\[3ex]
r = \dfrac{LSA}{2\pi h} \\[5ex]
h = \dfrac{LSA}{2\pi r} \\[5ex]
LSA = \pi dh \\[3ex]
h = \dfrac{LSA}{\pi d} \\[5ex]
d = \dfrac{LSA}{\pi h} \\[5ex]
BA = \pi r^2 \\[3ex]
r = \dfrac{\sqrt{\pi BA}}{\pi} \\[5ex]
r = \dfrac{1}{\pi} * \sqrt{\dfrac{\pi(TSA - 2 * LSA)}{2}} \\[5ex]
BA = \dfrac{\pi d^2}{4} \\[5ex]
d = \dfrac{2\sqrt{\pi BA}}{\pi} \\[5ex]
d = \dfrac{\sqrt{2\pi (TSA - LSA)}}{\pi} \\[5ex]
TSA = 2\pi r(r + h) \\[3ex]
h = \dfrac{TSA - 2\pi r^2}{2\pi r} \\[5ex]
r = \dfrac{-\pi h \pm \sqrt{\pi(\pi h^2 + 2 * TSA)}}{2\pi} \\[5ex]
TSA = 2BA + LSA \\[3ex]
BA = \dfrac{TSA - LSA}{2} \\[5ex]
LSA = TSA - 2BA \\[3ex]
TSA = \pi d\left(\dfrac{d + 2h}{2}\right) \\[5ex]
h = \dfrac{2 * TSA - \pi d^2}{2\pi d} \\[5ex]
d = \dfrac{-\pi h \pm \sqrt{\pi(h^2 + 2 * TSA)}}{\pi} \\[5ex]
h = \dfrac{LSA * \sqrt{\pi * BA}}{\pi * BA} \\[5ex]
h = \dfrac{LSA}{\sqrt{2\pi(TSA - LSA)}} \\[5ex]
BA = \dfrac{LSA^2}{\pi h^2} \\[5ex]
BA = \dfrac{(4 * TSA + \pi h^2) \pm h\sqrt{\pi(\pi h^2 - 8 * TSA)}}{8} \\[5ex]
LSA = h\sqrt{BA * \pi} \\[3ex]
LSA = \dfrac{-\pi h^2 \pm h\sqrt{\pi(\pi h^2 + 8 * TSA)}}{4} \\[5ex]
TSA = 2 * BA \pm h\sqrt{\pi * BA} \\[3ex]
TSA = \dfrac{LSA(2 * LSA + \pi h^2)}{\pi h^2} \\[5ex]
V = \pi r^2h \\[3ex]
r = \dfrac{2V}{LSA} \\[5ex]
d = \dfrac{4V}{LSA} \\[5ex]
r = \dfrac{\sqrt{Vh\pi}}{h\pi} \\[5ex]
V = BA * h \\[3ex]
BA = \dfrac{V}{h} \\[5ex]
h = \dfrac{V}{BA} \\[5ex]
h = \dfrac{V}{\pi r^2} \\[5ex]
h = \dfrac{4V}{\pi d^2} \\[5ex]
V = \dfrac{\pi d^2h}{4} \\[5ex]
d = \dfrac{\sqrt{Vh\pi}}2{h\pi} \\[5ex]
V = \dfrac{LSA^2}{h\pi} \\[5ex]
LSA = \sqrt{Vh\pi} \\[3ex]
h = \dfrac{LSA^2}{4V\pi} \\[5ex]
V = \dfrac{(h^3\pi + 4 * TSA * h) \pm h^2\sqrt{\pi(h^2\pi + 8 * TSA)}}{8} \\[5ex]
TSA = \dfrac{2V + h\sqrt{Vh\pi}}{h} \\[5ex]
TSA = \dfrac{2V + 2\pi rh^2}{h} \\[5ex]
r = \dfrac{TSA * h - 2V}{2\pi h^2} \\[5ex]
d = \dfrac{TSA * h - 2V}{\pi h^2} \\[5ex]
h = \dfrac{TSA \pm \sqrt{TSA^2 - 16\pi rV}}{4\pi r}
$
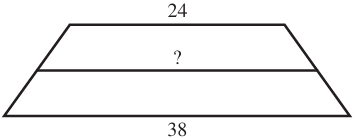
Trapezoid
Trapezoid's Midpoint Segment Theorem states that the line segment connecting the nonparallel sides of a
trapezoid is parallel to the bases, and it's length is the average of the lengths of the bases.
$
Midline = \dfrac{short\;\;base + long\;base}{2}
$
Which of the following represents the area, in square centimeters, of the shaded region?
$ A.\;\; 32 - 8\pi \\[3ex] B.\;\; 32 - 16\pi \\[3ex] C.\;\; 32 + 16\pi \\[3ex] D.\;\; 64 - 16\pi \\[3ex] E.\;\; 64 + 16\pi \\[3ex] $
Area of the shaded region = Area of the Square − Area of the Circle
$ \underline{Square} \\[3ex] apothem,\;a = 4\;cm \\[3ex] Length,\;L = 2a = 2(4) = 8\;cm \\[3ex] Area,\;A = L^2 \\[3ex] A = 8^2 \\[3ex] A = 64\;cm^2 \\[5ex] \underline{Circle} \\[3ex] radius,\;r = 4\;cm \\[3ex] Area,\;A = \pi r^2 \\[4ex] A = \pi(4)^2 \\[4ex] A = 16\pi\;cm^2 \\[5ex] \implies \\[3ex] \text{Area of the shaded region} = 64 - 16\pi $
She will order materials from a website that offers 4 different print designs and 4 different color schemes that can be used with each design.
The top and bottom edges of Josie’s current lampshade are parallel circles with diameters of length 6 inches and 8 inches, as pictured below.
The centers of the 2 circles are directly above and below one another.
(I.) What is the ratio of the area of the circle modeled by the top edge of the lampshade to the area of the circle modeled by the bottom edge of the lampshade?
$ A.\;\; 3:7 \\[3ex] B.\;\; 3:4 \\[3ex] C.\;\; 9:16 \\[3ex] D.\;\; 4:3 \\[3ex] E.\;\; 16:9 \\[5ex] $ (II.) Which of the following 2-dimensional shapes, when rotated about its vertical symmetry line, will form the shape of this lampshade?
A. Circle
B. Octagon
C. Pentagon
D. Rectangle
E. Isosceles trapezoid
(I.) Let:
r be the radius of the circle modeled by the top edge of the lampshade
R be teh radius of the circle modeled by the bottom edge of the lampshade
$ radius = \dfrac{diameter}{2} \\[5ex] Area = \pi radius^2 \\[4ex] r = \dfrac{6}{2} = 3\;in \\[5ex] R = \dfrac{8}{2} = 4\;in \\[5ex] \text{Ratio of the areas} \\[3ex] = \dfrac{\pi (3)^2}{\pi (4)^2} \\[5ex] = \dfrac{9}{16} \\[5ex] = 9 : 16 \\[3ex] $ (II.) The shape of Josie's lampshade is a truncated cone.
When rotated about its vertical symmetry line, the 2-dimensional shape that will form the shape of a truncated cone is the Isosceles trapezoid.
The top of the rack is in the shape of a trapezoid.
The trapezoid's bases are 24 inches long and 38 inches long, respectively.
Tisha will add a brace that joins the midpoints of the trapezoid's 2 nonparallel sides to support her drying rack, as shown in the figure below.
How many inches long will the brace be?
$ A.\;\; 26 \\[3ex] B.\;\; 28 \\[3ex] C.\;\; 31 \\[3ex] D.\;\; 32 \\[3ex] E.\;\; 33.5 \\[3ex] $
$ Midline = \dfrac{short\;\;base + long\;base}{2} ...Midpoint\;\;Segment\;\;Theorem \\[5ex] = \dfrac{24 + 38}{2} \\[5ex] = \dfrac{62}{2} \\[5ex] = 31\;inches $
Which of the following expressions must give the area of the shaded region, in square meters?
$ A.\;\; ab - cd \\[3ex] B.\;\; ab - ef \\[3ex] C.\;\; cd - ef \\[3ex] D.\;\; cd + ef \\[3ex] E.\;\; ab - cd + ef \\[3ex] $
$ \text{Area of a rectangle} = Length \cdot Width \\[3ex] \text{Area of the 1st (inner) rectangle},A_1 = f \cdot e = ef \\[4ex] \text{Area of the 2nd rectangle}, A_2 = d \cdot c = cd \\[4ex] \text{Area of the shaded region} = A_2 - A_1 \\[4ex] = cd - ef $
What is the area, in square coordinate units, of $\triangle PQR$?
$ F.\;\; 6 \\[3ex] G.\;\; 10 \\[3ex] H.\;\; 12 \\[3ex] J.\;\; 20 \\[3ex] K.\;\; 48 \\[3ex] $
$ P:\;Vertex\;1:\;\;(x_1, y_1) = (8, 12) \\[4ex] Q:\;Vertex\;2:\;\;(x_2, y_2) = (10, 8) \\[4ex] R:\;Vertex\;3:\;\;(x_3, y_3) = (8, 2) \\[4ex] x_1 = 8 ~~~~~~~~~~~~~~~~ y_1 = 12 \\[4ex] x_2 = 10 ~~~~~~~~~~~~~~~ y_2 = 8 \\[4ex] x_3 = 8 ~~~~~~~~~~~~~~~~~ y_3 = 2 \\[4ex] Area = \dfrac{1}{2}|x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| \\[4ex] = \dfrac{1}{2}|8(8 - 2) + 10(2 - 12) + 8(12 - 8)| \\[5ex] = \dfrac{1}{2}|8(6) + 10(-10) + 8(4)| \\[5ex] = \dfrac{1}{2}|48 - 100 + 32| \\[5ex] = \dfrac{1}{2}|-20| \\[5ex] = \dfrac{1}{2} \cdot 20 \\[5ex] = 10\;square\;\;units $
$ A.\;\; D = S \\[3ex] B.\;\; D = \sqrt{2}S \\[3ex] C.\;\; D = \sqrt{3}S \\[3ex] D.\;\; D = 2S \\[3ex] E.\;\; D = 3S \\[3ex] $
The four sides of the square are congruent
Each interior angle in a square is a right angle
$ \underline{\triangle ABC} \\[3ex] hyp^2 = leg^2 + leg^2 ...\text{Pythagorean Theorem} \\[4ex] D^2 = S^2 + S^2 \\[4ex] D^2 = 2S^2 \\[4ex] D = \sqrt{2S^2} \\[4ex] D = \sqrt{2} \cdot \sqrt{S^2} \\[4ex] D = \sqrt{2}S $
Each pair of adjacent walls meets at a right angle.
Teresa plans to completely carpet this entire hallway floor.
At a cost of $2 per square foot, how much will carpeting this hallway floor cost?
$ A.\;\; \$ 95 \\[3ex] B.\;\; \$ 150 \\[3ex] C.\;\; \$ 190 \\[3ex] D.\;\; \$ 285 \\[3ex] E.\;\; \$ 300 \\[3ex] $
15 feet − 4 feet = 11 feet
Hence we have two regions: Region 1 and Region 2
$ \text{Area of Region 1 } = 4(10) = 40\;feet^2 \\[4ex] \text{Area of Region 2 } = 11(5) = 55\;feet^2 \\[4ex] \text{Area of Hallway Floor} = \text{Area of Region 1} + \text{Area of Region 2} \\[3ex] = 40 + 55 \\[3ex] = 95\;feet^2 \\[5ex] \text{Cost of Carpeting Entire Hallway Floor } @\;\;\$2\;\; \text{per square feet } \\[3ex] = 95\;square\;\;feet \cdot \dfrac{\$2}{1\;square\;\;foot} \\[5ex] = \$ 190 $
The square section measures 20feet on each side.
The pond touches all 4 sides of the square section.
Approximately what is the total area, in square feet, of the region inside this square section but outside the circular pond?
$ A.\;\; 86 \\[3ex] B.\;\; 126 \\[3ex] C.\;\; 314 \\[3ex] D.\;\; 337 \\[3ex] E.\;\; 714 \\[3ex] $
Let us represent this information diagrammatically
O is the center of the circle.
The region inside this square section but outside the circular pond is the shaded region.
The question is asking us to calculate the area of the shaded region.
$ \underline{\text{Square Section}} \\[3ex] \text{Length of the square} = 20\;feet \\[3ex] Area = Length^2 \\[4ex] = 20^2 \\[3ex] = 400\;feet^2 \\[5ex] \underline{\text{Circular Pond}} \\[3ex] \text{radius of the circle} = \dfrac{1}{2} \cdot 20 = 10\;feet ...\text{radius of an inscribed circle = half the length of the square} \\[5ex] Area = \pi * radius^2 \\[4ex] = \pi * 10^2 \\[4ex] = 100\pi \\[5ex] \underline{\text{Area of the shaded region}} \\[3ex] = \text{Area of the Square Section} - \text{Area of the Circular Pond} \\[3ex] = 400 - 100\pi \\[3ex] = 85.84073464 \\[3ex] \approx 86\;feet^2 ...\text{to the nearest whole number} $
He tied a decorative rope around it and used an extra 6 inches for a tie at the top, as shown below.
On both the top and the bottom, he formed right angles where the rope crossed.
About how many inches of decorative rope did Rafael use?
$ F.\;\; 2l + 2w + 2h \\[3ex] G.\;\; 2l + 2w + 2h + 6 \\[3ex] H.\;\; 2l + 2w + 4h + 6 \\[3ex] J.\;\; 2l + 4w + 2h + 6 \\[3ex] K.\;\; 4l + 2w + 2h + 6 \\[3ex] $
$ \text{Decorative Rope} \\[5ex] \underline{\text{Top and Bottom of Box}} \\[3ex] Length:\;\; 2 \cdot l = 2l\;inches \\[3ex] Width:\;\; 2 \cdot w = 2w\;inches \\[5ex] \underline{\text{4 Sides of the Box}} \\[3ex] Height:\;\; 4 \cdot h = 4h\;inches \\[5ex] \underline{\text{Extra 6 inches for a tie at the top}} \\[3ex] Tie:\;\; 6\;inches \\[5ex] \text{Perimeter of Decorative Rope} = (2l + 2w + 4h + 6)\;inches $
Let a and b be the volumes of A and B, respectively.
Which of the following equations is true?
$ F.\;\; a = \dfrac{1}{3}b \\[5ex] G.\;\; a = \dfrac{2}{3}b \\[5ex] H.\;\; a = b \\[3ex] J.\;\; a = \dfrac{3}{2}b \\[5ex] K.\;\; a = 3b \\[3ex] $
$ \underline{Rectangular\;\;Pyramid} \\[3ex] Volume = \dfrac{1}{3} \cdot Length \cdot Width \cdot \perp Height \\[5ex] a = \dfrac{1}{3} \cdot \dfrac{12}{x} \cdot x \cdot 12 \\[5ex] a = 48\;cubic\;feet \\[5ex] b = \dfrac{1}{3} \cdot 12 \cdot x \cdot \dfrac{12}{x} \\[5ex] b = 48\;cubic\;feet \\[5ex] a = b $
A. 6
B. 12
C. 15
D. 25
E. 30
We can solve this question using at least two approaches.
Use any approach you prefer.
$ \text{1st Approach: Hero's Formula} \\[3ex] side1, a = 5\;mm \\[3ex] side2, b = 5\;mm \\[3ex] side3, c = 6\;mm \\[3ex] semiperimeter, s = \dfrac{a + b + c}{2} \\[5ex] = \dfrac{5 + 5 + 6}{2} \\[5ex] = \dfrac{16}{2} \\[5ex] = 8\;mm \\[5ex] difference1 = semiperimeter - side1 \\[3ex] = s - a \\[3ex] = 8 - 5 \\[3ex] = 3\;mm \\[5ex] difference2 = semiperimeter - side2 \\[3ex] = s - b \\[3ex] = 8 - 5 \\[3ex] = 3\;mm \\[5ex] difference3 = semiperimeter - side3 \\[3ex] = s - c \\[3ex] = 8 - 6 \\[3ex] = 2\;mm \\[5ex] Area, A = \sqrt{s(s - a)(s - b)(s - c)} \\[4ex] = \sqrt{8(3)(3)(2)} \\[4ex] = \sqrt{144} \\[4ex] = 12\;mm^2 \\[5ex] \text{2nd Approach: Formula and Theorem} \\[3ex] $ To do the 2nd approach, let us represent the information diagrammatically.
Draw a perpendicular line from Vertex B to Midpoint D
base = b = 6mm
perpendicular height = h
$ 5^2 = h^2 + 3^2 ...\text{Pythagorean Theorem} \\[4ex] 25 = h^2 + 9 \\[4ex] h^2 + 9 = 25 \\[4ex] h^2 = 25 - 9 \\[4ex] h^2 = 16 \\[4ex] h = \sqrt{16} \\[4ex] h = 4\;mm \\[5ex] Area, A = \dfrac{1}{2} \cdot b \cdot h \\[5ex] = \dfrac{1}{2} \cdot 6 \cdot 4 \\[5ex] = 12\;mm^2 $
What is the area, in square coordinate units, of $\triangle PQR$?
$ A.\;\; 18 \\[3ex] B.\;\; 21 \\[3ex] C.\;\; 36 \\[3ex] D.\;\; 40 \\[3ex] E.\;\; 42 \\[3ex] $
$ P:\;Vertex\;1:\;\;(x_1, y_1) = (8, 10) \\[4ex] Q:\;Vertex\;2:\;\;(x_2, y_2) = (8, 4) \\[4ex] R:\;Vertex\;3:\;\;(x_3, y_3) = (1, 2) \\[4ex] x_1 = 8 ~~~~~~~~~~~~~~~~ y_1 = 10 \\[4ex] x_2 = 8 ~~~~~~~~~~~~~~~ y_2 = 4 \\[4ex] x_3 = 1 ~~~~~~~~~~~~~~~~~ y_3 = 2 \\[4ex] Area = \dfrac{1}{2}|x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| \\[4ex] = \dfrac{1}{2}|8(4 - 2) + 8(2 - 10) + 1(10 - 4)| \\[5ex] = \dfrac{1}{2}|8(2) + 8(-8) + 1(6)| \\[5ex] = \dfrac{1}{2}|16 - 64 + 6| \\[5ex] = \dfrac{1}{2}|-42| \\[5ex] = \dfrac{1}{2} \cdot 42 \\[5ex] = 21\;square\;\;units $
The given lengths are in centimeters.
Which of the following values is closest to the perimeter, in centimeters, of ABCD?
$ F.\;\; 32 \\[3ex] G.\;\; 40 \\[3ex] H.\;\; 65 \\[3ex] J.\;\; 91 \\[3ex] K.\;\; 182 \\[3ex] $
Considering the fact that you have to solve this question in 1 minute, it is recommended that you figure out the correct answer.
This is because the figure is drawn to scale
1st Approach:
In Figure ABE, the hypotenuse, |AB| is greater than 24
Assume that |AB| is about 25 cm
This also means that |AD| is about 25 cm
In Figure CBE, the hypotenuse, |CB| is greater than 7
Assume that |CB| is about 8 cm
This also means that |CD| is about 8 cm
So, the perimeter is about: 25(2) + 8(2) = 50 + 16 = 66 cm.
The closest answer in the option is 65 cm.
So, the correct answer is Option H.
$ \underline{\text{2nd Approach}} \\[3ex] \underline{\text{Right Triangles and the Pythagorean Theorem}} \\[3ex] \underline{\triangle ABE} \\[3ex] hyp^2 = 24^2 + 7^2 \\[4ex] hyp^2 = 576 + 49 \\[4ex] hyp = \sqrt{625} \\[3ex] |AB| = hyp = 25\;cm \\[5ex] \underline{\triangle ADE} \\[3ex] |AD| = hyp = 25\;cm ...\text{congruent triangle to triangle ABE} \\[5ex] \underline{\triangle BCE} \\[3ex] hyp^2 = 7^2 + 2^2 \\[4ex] hyp^2 = 49 + 4 \\[3ex] hyp = \sqrt{53} \\[3ex] |BC| = hyp = 7.280109889\;cm \\[5ex] \underline{\triangle DCE} \\[3ex] |DC| = hyp = 7.280109889\;cm ...\text{congruent triangle to triangle BCE} \\[5ex] Perimeter = |AB| + |AD| + |BC| + |DC| \\[3ex] = 25 + 25 + 7.280109889 + 7.280109889 \\[3ex] = 64.56021978 \\[3ex] \approx 65\;cm $
All lines that meet in the figure do so at right angles.
Which of the following values is closest to the area, in square feet, of the 1 service box shown shaded?
$ F.\;\; 284 \\[3ex] G.\;\; 527 \\[3ex] H.\;\; 567 \\[3ex] J.\;\; 1,053 \\[3ex] K.\;\; 1,134 \\[3ex] $
Dimensions of shaded box = 21 feet by 13.5 feet
Length = 21 feet
Width = 13.5 feet
$ Area = Length \cdot Width \\[3ex] = 21 \cdot 13.5 \\[3ex] = 283.5 \\[3ex] \approx 284\;square\;feet $
What is the area, in square coordinate units, of ▵PQR?
$ A.\;\; 6 \\[3ex] B.\;\; 10 \\[3ex] C.\;\; 12 \\[3ex] D.\;\; 15 \\[3ex] E.\;\; 30 \\[3ex] $
$ P:\;Vertex\;1:\;\;(x_1, y_1) = (7, 6) \\[4ex] Q:\;Vertex\;2:\;\;(x_2, y_2) = (7, 3) \\[4ex] R:\;Vertex\;3:\;\;(x_3, y_3) = (-3, 4) \\[4ex] x_1 = 7 \hspace{5em} y_1 = 6 \\[4ex] x_2 = 7 \hspace{5em} y_2 = 3 \\[4ex] x_3 = -3 \hspace{5em} y_3 = 4 \\[4ex] Area = \dfrac{1}{2}|x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| \\[4ex] = \dfrac{1}{2}|7(3 - 4) + 7(4 - 6) + -3(6 - 3)| \\[5ex] = \dfrac{1}{2}|7(-1) + 7(-2) - 3(3)| \\[5ex] = \dfrac{1}{2}|-7 - 14 - 9| \\[5ex] = \dfrac{1}{2}|-30| \\[5ex] = \dfrac{1}{2} \cdot 30 \\[5ex] = 15\;square\;\;units $
Which of the following expressions gives the area, in square meters, of $\triangle ABC$?
$ A.\;\; hb \\[3ex] B.\;\; \dfrac{1}{2}ab \\[5ex] C.\;\; c\sin A \\[3ex] D.\;\; abc \sin A \\[3ex] E.\;\; \dfrac{1}{2}bc\sin A \\[5ex] $
$ \underline{\text{Area of a Triangle}} \\[3ex] Area = \dfrac{1}{2} \cdot base \cdot \perp height...\text{usually given to you} \\[5ex] \text{However, please see this pattern in another formula for Area} \\[3ex] Area = \dfrac{1}{2}ab \sin C \\[5ex] or \\[3ex] Area = \dfrac{1}{2}ac \sin B \\[5ex] or \\[3ex] Area = \dfrac{1}{2} bc \sin A \\[5ex] $ The correct answer is Option E.
Did you notice the pattern in the area: $\dfrac{1}{2} \cdot \;...$
sides: ab; Angle: C
sides: ac; Angle: B
sides: bc; Angle: A
Student: What if I do not remember the second formula?
ACT gives only the first formula.
$\dfrac{base \times height}{2}$ ...this is the formula that I am familiar with
Teacher: In that case, let us use the first formula and get the second formula.
Let us insert another label, D...vertex B meets $\overline{AC}$ at D
$ \underline{\triangle ABD} \\[3ex] SOHCAHTOA \\[3ex] \sin A = \dfrac{opp}{hyp} = \dfrac{h}{c} \\[5ex] h = c\sin A \\[5ex] Area = \dfrac{1}{2}bh \\[5ex] = \dfrac{1}{2} \cdot b \cdot c\sin A \\[5ex] = \dfrac{1}{2}bc\sin A $
The paper towels come in boxes of 6 rolls with a shipping weight of 6.8 pounds.
The cost for a box of 6 rolls of this paper towel is $15.99 plus the shipping cost, given in the table below.
| Number of boxes shipped | Shipping cost per box |
|---|---|
|
1 – 10 11 – 99 100 or more |
$13.25 $12.00 $10.00 |
The diameter of each cylindrical roll is 6 inches.
Each roll has a cylindrical hole 1.5 inches in diameter, and each roll has a height of 11 inches, as shown in the diagrams below.
The 6 rolls are shipped in a box as shown below where the interior of the box is as small as possible.
What are the interior dimensions of this box, in inches?
$ A.\;\; 8 \times 12 \times 11 \\[3ex] B.\;\; 9 \times 13.5 \times 11 \\[3ex] C.\;\; 11 \times 16.5 \times 11 \\[3ex] D.\;\; 12 \times 18 \times 11 \\[3ex] E.\;\; 36 \times 36 \times 66 \\[3ex] $
Length: 2 rolls * 6 inches diameter = 12 inches
Width: 3 rolls * 6 inches diameter = 18 inches
Height: 1 roll of 11 inches (all the rolls have equal height)
The interior dimensions of the box = Length × Width × Height
= 12 inches × 18 inches × 11 inches
The volume of the large prism is the same as the volume of how many of the small prisms?
$ A.\;\; 2 \\[3ex] B.\;\; 4 \\[3ex] C.\;\; 6 \\[3ex] D.\;\; 7 \\[3ex] E.\;\; 12 \\[3ex] $
$ \text{Volume of a rectangular prism} = Length \cdot Width \cdot Height \\[3ex] \underline{\text{Small Prism}} \\[3ex] Volume_{small} = x \cdot y \cdot z \\[3ex] Volume_{small} = xyz \\[5ex] \underline{\text{Large Prism}} \\[3ex] Volume_{large} = 2x \cdot 2y \cdot 3z \\[3ex] Volume_{large} = 2\cdot x \cdot 2\cdot y \cdot 3\cdot z \\[3ex] Volume_{large} = 12xyz \\[5ex] $ $Volume_{large}$ is equal to how many of $Volume_{small}?$
$ Volume_{large} = \text{how many} \;\; Volume_{small} \\[3ex] 12xyz = \text{how many} \cdot xyz \\[3ex] \text{how many} = \dfrac{12xyz}{xyz} \\[5ex] how many = 12 $
Points C and D are on $\overline{BE}$ such that $\overline{BC}$, $\overline{CD}$, and $\overline{DE}$ all have the same length.
Points F and G are on $\overline{EH}$ such that $\overline{EF}$, $\overline{FG}$, and $\overline{GH}$ all have the same length.
How many of the triangles numbered 1 – 5 ($\triangle ABC$, $\triangle ACD$, $\triangle ADE$, $\triangle AEF$, and $\triangle AFG$ respectively) have the same area as $\triangle AGH$?
$ A.\;\; 1 \\[3ex] B.\;\; 2 \\[3ex] C.\;\; 3 \\[3ex] D.\;\; 4 \\[3ex] E.\;\; 5 \\[3ex] $
Let us analyze this question.
$ \text{Area of a Triangle} = \dfrac{1}{2} \cdot base \cdot \perp height \\[3ex] $ $\triangle ACB$ has the same area as $\triangle AGH$
This is because they have:
(I.) the same base: $\overline{BC} = \overline{GH}$
(II.) the same perpendicular height: because a square has equal sides: $\overline{AB} = \overline{AH}$
The other triangles: $\triangle ACD$, $\triangle ADE$, $\triangle AEF$, and $\triangle AFG$ have:
(III.) the same base: $\overline{CD} = \overline{DE} = \overline{EF} = \overline{FG}$
But what about their perpendicular heights?
How do we calculate the area of a triangle if the triangle does not have a perpendicular height?
One of the ways to calculate the area is to extend the base to the same level as the opposite vertex, then draw a perpendicular height from that vertex to the extension of the base.
This is what I mean.
$\triangle ACD$ does not a perpendicular height
One of the ways to calculate the area of the triangle is to draw the perpendicular height $\overline{AB}$ (Please see the red lines)
This implies that the perpendicular height is still the same side of the square
(IV.) the same perpendicular height: the side of the square
Therefore all five triangles: $\triangle ACB$, $\triangle ACD$, $\triangle ADE$, $\triangle AEF$, and $\triangle AFG$ have the same area as $\triangle AGH$.
The trapezoid consists of a right triangle and a square divided into 3 isosceles right triangles.
The unshaded regions will be white rock; the shaded triangular regions will be black rock.
What is the area, in square meters, that will be black rock?
$ F.\;\; 20 \\[3ex] G.\;\; 25 \\[3ex] H.\;\; 45 \\[3ex] J.\;\; 60 \\[3ex] K.\;\; 70 \\[3ex] $
The diagram is drawn to scale.
Doing it the ACT way (because of the time limit of 1 minute):
$ \underline{\text{shaded right triangle}} \\[3ex] base = 14 - 10 = 4\;m \\[3ex] \perp height = 10\;m \\[3ex] Area = \dfrac{1}{2} \cdot base \cdot \perp height \\[5ex] = \dfrac{1}{2} \cdot 4 \cdot 10 = 20\;m^2 \\[5ex] \underline{\text{shaded isosceles triangle}} \\[3ex] Area = \dfrac{1}{4} \cdot \text{Area of the square}...diagram \\[3ex] = \dfrac{1}{4} \cdot (10 \cdot 10) \\[5ex] = 25\;m^2 \\[5ex] \underline{\text{black rock}} \\[3ex] Area = 20 + 25 \\[3ex] = 45\;m^2 \\[3ex] $
The side length of square ABCD is 14 meters.
What is the area, in square meters, of the shaded portion?
$ F.\;\; 7\sqrt{2} \\[3ex] G.\;\; 14\sqrt{2} \\[3ex] H.\;\; 24.5 \\[3ex] J.\;\; 49 \\[3ex] K.\;\; 98 \\[3ex] $
Area of the shaded portion = Area of Square ABCD − Area of Square KLMN
Area of a Square = Side Length²
$ \underline{\text{Square ABCD}} \\[3ex] \text{side length} = 14\;m \\[3ex] \overline{AB} = \overline{BC} = \overline{CD} = \overline{DA} = 14\;m \\[3ex] Area = 14^2 \\[3ex] Area = 196\;m^2 \\[5ex] \underline{\text{Triangle ALK}} \\[3ex] \text{This is a right triangle because a square has 4 right angles} \\[3ex] \overline{AL} = \dfrac{\overline{AB}}{2} ...\text{Midpoint} \\[5ex] = \dfrac{14}{2} \\[5ex] = 7\;m \\[5ex] \overline{AK} = \dfrac{\overline{DA}}{2} ...\text{Midpoint} \\[5ex] = \dfrac{14}{2} \\[5ex] = 7\;m \\[5ex] \overline{KL}^2 = \overline{AL}^2 + \overline{AK}^2 ...\text{Pythagorean Theorem} \\[3ex] \overline{KL}^2 = 7^2 + 7^2 \\[3ex] \overline{KL}^2 = 49 + 49 \\[3ex] \overline{KL}^2 = 98 \\[3ex] \overline{KL} = \sqrt{98} \\[5ex] \underline{\text{Square KLMN}} \\[3ex] \text{side length} = \overline{KL} = \sqrt{98}\;m \\[3ex] Area = \sqrt{98}^2 \\[3ex] Area = 98\;m^2 \\[5ex] \underline{\text{Shaded Portion}} \\[3ex] Area = 196 - 98 \\[3ex] Area = 98\;m^2 $
Shown below is quadrilateral ABCD in the standard (x, y) coordinate plane.
What is b, the length of the other base, in feet?
$ F.\;\; 6 \\[3ex] G.\;\; 8 \\[3ex] H.\;\; 13 \\[3ex] J.\;\; 15 \\[3ex] K.\;\; 23 \\[3ex] $
The area of a trapezoid is the product of: one-half and the sum of the parallel sides and the perpendicular height
$ Area = 20\;ft^2 \\[3ex] Area = \dfrac{1}{2} \cdot (2 + b) \cdot 5 \\[5ex] \dfrac{5}{2} \cdot (2 + b) = 20 \\[5ex] 2 + b = 20 \cdot \dfrac{2}{5} \\[5ex] 2 + b = 8 \\[3ex] b = 8 - 2 \\[3ex] b = 6\;feet $
Jerry is building a rectangular patio against one side of his house.
The top surface of the patio, along with its width and diagonal, is shown in the figure below.
To build the patio, he will first dig a rectangular hole to a uniform depth of 8 inches.
He will then fill the hole with gravel to a uniform depth of 3 inches.
He will purchase gravel from his local rock quarry for $54 per cubic yard (1 cubic yard = 27 cubic feet).
Next, he will pour concrete on top of the gravel to obtain a smooth surface for the patio.
Finally, he will frame and build a rectangular concrete step with the dimensions shown below.
