☰ Please Read Me.

BISE-Multan: 10th Grade: General Mathematics Objective Tests

Welcome to Our Site


I greet you this day,
These are the solutions to the General Mathematics multiple-choice questions on the Objective Tests of the Board of Intermediate and Secondary Education, Multan.
The link to the video solutions will be provided for you. Please subscribe to the YouTube channel to be notified of upcoming livestreams. You are welcome to ask questions during the video livestreams.
If you find these resources valuable and if any of these resources were helpful in your passing the BISE General Mathematics tests/exams, please consider making a donation:

Cash App: $ExamsSuccess or
cash.app/ExamsSuccess

PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess

Google charges me for the hosting of this website and my other educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well. As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.

Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.

(1.) $a^3 + 3ab(a + b) + b^3$ = ?

$ A.\;\; (a + b)^3 \\[3ex] B.\;\; (a - b)^3 \\[3ex] C.\;\; a^3 + b^3 \\[3ex] D.\;\; a^3 - b^3 \\[3ex] $

$ a^3 + 3ab(a + b) + b^3 \\[3ex] = a^3 + 3a^2b + 3ab^2 + b^3 \\[5ex] (a + b)^3 \\[3ex] \text{Pascal's Triangle: }\;\;1 \hspace{3em} 3 \hspace{3em} 3 \hspace{3em} 1 \\[3ex] = 1a^3 + 3a^2(b) + 3a(b)^2 + 1(b)^3 \\[3ex] = a^3 + 3a^2b + 3ab^2 + b^3 \\[5ex] \therefore a^3 + 3ab(a + b) + b^3 = (a + b)^3 $
(2.) $\sqrt{a} = a^{\dfrac{1}{2}}$ is a surd of order:

$ A.\;\; 0 \\[3ex] B.\;\; 2 \\[3ex] C.\;\; \dfrac{1}{2} \\[5ex] D.\;\; 1 \\[3ex] $

A surd is of the form: $\sqrt[index]{radicand}$ where the radical is the root symbol: √
The order of a surd is the index of it's radical: the number written above the root symbol.
Square roots has index of 2
Hence, the order of $\sqrt{a} = \sqrt[2]{a} = 2$
(3.) Factorization of $x^4 - 16$ is:

$ A.\;\; (x - 2)(x - 2) \\[3ex] B.\;\; (x - 4)(x - 4) \\[3ex] C.\;\; (x - 2)(x + 2)(x^2 + 4) \\[3ex] D.\;\; (x - 2)(x + 4) \\[3ex] $

$ x^4 - 16 \\[4ex] = (x^2)^2 - 4^2 \\[4ex] = (x^2 + 4)(x^2 - 4)...\text{Difference of Two Squares} \\[4ex] ..............................................\\[3ex] x^2 - 4 \\[3ex] = x^2 - 2^2 \\[3ex] = (x + 2)(x - 2) ...\text{Difference of Two Squares} \\[3ex] ..............................................\\[3ex] = (x^2 + 4)(x + 2)(x - 2) $
(4.) A linear polynomial is of degree:

A. 0
B. 1
C. 2
D. 3


A linear polynomial is of degree: 1
(5.) Solution set of $|x - 3| = 5$ is:

$ A.\;\; \{-8, 2\} \\[3ex] B.\;\; \{8, 2\} \\[3ex] C.\;\; \{-8, -2\} \\[3ex] D.\;\; \{8, -2\} \\[3ex] $

$ |x - 3| = 5 \\[3ex] x - 3 = 5 \hspace{1em}OR\hspace{1em} -(x - 3) = 5 \\[3ex] x = 5 + 3 \hspace{1em}OR\hspace{1em} x - 3 = -5 \\[3ex] x = 8 \hspace{1em}OR\hspace{1em} x = -5 + 3 \\[3ex] x = 8 \hspace{1em}OR\hspace{1em} x = -2 \\[3ex] \text{Solution Set} = \{8, -2\} $
(6.) In a square matrix, the number of rows and columns are:

A. 2 × 3
B. 3 × 2
C. Same
D. Different


A square matrix is a matrix with equal number of rows of columns.
In a square matrix, the number of rows and columns are: Same.
(7.) Solution set of $x^2 - 9 = 0$

$ A.\;\; \{9\} \\[3ex] B.\;\; \{\pm 9\} \\[3ex] C.\;\; \{3\} \\[3ex] D.\;\; \{\pm 3\} \\[3ex] $

$ x^2 - 9 = 0 \\[3ex] x^2 = 9 \\[3ex] x = \pm\sqrt{9} \\[3ex] x = \pm 3 $
(8.) In matrices $(AB)^{-1} = ?$

$ A.\;\; A^{-1} \\[3ex] B.\;\; B^{-1} \\[3ex] C.\;\; A^{-1}B^{-1} \\[3ex] D.\;\; B^{-1}A^{-1} \\[3ex] $

$ (AB)^{-1} = B^{-1} * A^{-1} $
(9.) $a^3 - 3ab(a - b) - b^3$ = ?

$ A.\;\; (a + b)^3 \\[3ex] B.\;\; (a - b)^3 \\[3ex] C.\;\; a^3 + b^3 \\[3ex] D.\;\; a^3 - b^3 \\[3ex] $

$ a^3 - 3ab(a - b) - b^3 \\[3ex] = a^3 - 3a^2b + 3ab^2 - b^3 \\[5ex] (a - b)^3 \\[3ex] \text{Pascal's Triangle: }\;\;1 \hspace{3em} 3 \hspace{3em} 3 \hspace{3em} 1 \\[3ex] = 1a^3 + 3a^2(-b) + 3a(-b)^2 + 1(-b)^3 \\[3ex] = a^3 - 3a^2b + 3ab^2 - b^3 \\[5ex] \therefore a^3 - 3ab(a - b) - b^3 = (a - b)^3 $
(10.) An arc greater than semi-circle is called:

A. Minor arc
B. Chord
C. Major arc
D. Diameter


A semi-circle is half of a circle.
An arc greater than semi-circle is a Major arc.
(11.) Solution of $x^2 - 5x + 6 = 0$ is:

$ A.\;\; \{3\} \\[3ex] B.\;\; \{2\} \\[3ex] C.\;\; \{2, 3\} \\[3ex] D.\;\; \{-2, -3\} \\[3ex] $

$ x^2 - 5x + 6 = 0 \\[3ex] (x - 2)(x - 3) = 0 \\[3ex] x - 2 = 0 \hspace{2em}OR\hspace{2em} x - 3 = 0 \\[3ex] x = 2 \hspace{2em}OR\hspace{2em} x = 3 \\[3ex] $ Check
$x = 2, 3$
LHS RHS
$ x^2 - 5x + 6 \\[3ex] x = 2 \\[3ex] 2^2 - 5(2) + 6 \\[3ex] 4 - 10 + 6 \\[3ex] 0 $
$ x^2 - 5x + 6 \\[3ex] x = 3 \\[3ex] 3^2 - 5(3) + 6 \\[3ex] 9 - 15 + 6 \\[3ex] 0 $ 		$0$
(12.) The medians of triangle are:

A. Concurrent
B. Collinear
C. Non-concurrent
D. 4


A triangle has three sides and three vertices.
This implies three diagonals.
All the three diagonals meet at a single point: the centroid.
This means that they are concurrent at the centroid.
(13.) H.C.F of $12pq, 8p^2q$ is:

$ A.\;\; 4pq \\[3ex] B.\;\; 4p^2q^2 \\[3ex] C.\;\; 4pq^2 \\[3ex] D.\;\; 4p^2q \\[3ex] $

The colors besides red indicate the common factors that should be counted only one time.
They are the only ones to be included in the calculation of the HCF.

$ 12pq = \color{black}{2} * \color{darkblue}{2} * 3 * \color{purple}{p} * \color{brown}{q} \\[3ex] 8p^2q = \color{black}{2} * \color{darkblue}{2} * 2 * \color{purple}{p} * p * \color{brown}{q} \\[5ex] HCF = \color{black}{2} * \color{darkblue}{2} * \color{purple}{p} * \color{brown}{q} \\[3ex] HCF = 4pq $
(14.) Area of a semi-circle is:

$ A.\;\; \dfrac{\pi r^2}{2} \\[5ex] B.\;\; \pi r^2 \\[3ex] C.\;\; \pi^2 r \\[3ex] D.\;\; 2\pi r \\[3ex] $

$ \text{Area of a circle} = \pi r^2 \\[3ex] \text{A semi-circle is half of a circle} \\[3ex] \therefore \text{Area of a semicircle} = \dfrac{\pi r^2}{2} $
(15.) L.C.M of $12p^3q^2, 8p^2q$ is:

$ A.\;\; 24pq^2 \\[3ex] B.\;\; 24p^3q \\[3ex] C.\;\; 12p^2q \\[3ex] D.\;\; 24p^3q^2 \\[3ex] $

The colors besides red indicate the common factors that should be counted only one time.
They are the only ones to be included in the calculation of the HCF.

$ 12p^3q^2 = \color{black}{2} * \color{darkblue}{2} * 3 * \color{purple}{p} * \color{brown}{p} * p * q * q \\[3ex] 8p^2q = \color{black}{2} * \color{darkblue}{2} * 2 * \color{purple}{p} * \color{brown}{p} \\[5ex] LCM = \color{black}{2} * \color{darkblue}{2} * \color{purple}{p} * \color{brown}{p} * 3 * p * q * q * 2 \\[3ex] LCM = 24p^3q^2 $
(16.) The co-ordinates of the origin are:

A. 0
B. (0, 0)
C. (1, 0)
D. (0, 1)


The co-ordinates of the origin are (0, 0)
(17.) In given figure, the value of x is:

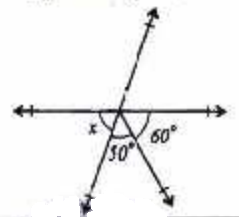
Number 17-2024

$ A.\;\; 50^\circ \\[3ex] B.\;\; 60^\circ \\[3ex] C.\;\; 110^\circ \\[3ex] D.\;\; 70^\circ \\[3ex] $

$ x + 50^\circ + 60^\circ = 180^\circ ...\text{sum of angles on a straight line} \\[3ex] x = 180 - 50 - 60 \\[3ex] x = 70^\circ $
(18.) Product of two expressions = ?

A. H.C.F
B. L.C.M
C. H.C.F × L.C.M
D. H.C.F + L.C.M


For any two numbers, the product of the two numbers is equal to the product of their Least Common Multiple (LCM) and Highest Common Factor (HCF).
(19.) Perimeter of a rectangle is:

$ A.\;\; 2(l \times w) \\[3ex] B.\;\; 2(l + w) \\[3ex] C.\;\; \dfrac{1}{2}(l \times w) \\[5ex] D.\;\; \dfrac{1}{2}(l + w) \\[5ex] $

$ \underline{Rectangle} \\[3ex] perimeter = P \\[3ex] length = l \\[3ex] width = w \\[3ex] P = l + l + w + w \\[3ex] P = 2l + 2w \\[3ex] P = 2(l + w) $
(20.) If $A^t = -A$ then A is called:

A. Symmetric
B. Skew symmetric
C. Transpose
D. Square matrix


A Skew symmetric matrix is a matrix that is equal to the negative of its transpose.
Say we have a matrix, $A$; matrix $A$ is a symmetric matrix if $A = -A^T$
(21.) Volume of a right circular cylinder is:

$ A.\;\; \dfrac{\pi r^2 h}{3} \\[5ex] B.\;\; \dfrac{\pi r^2 h}{2} \\[5ex] C.\;\; \pi r^2 h \\[3ex] D.\;\; \dfrac{4}{3}\pi r^2 \\[5ex] $

The volume of a cylinder can be considered as the stacking of circular layers (circles) along the height of the cylinder.
So, the volume can be considered as the product of the base area and the height.

$ \text{base area} = BA \\[3ex] radius = r \\[3ex] height = h \\[3ex] volume = V \\[5ex] \underline{\text{Right Circular Cylinder}} \\[3ex] \text{The base area is a circle} \\[3ex] \therefore \text{The base area is the area of a circle} \\[3ex] BA = \pi r^2 \\[5ex] V = BA * h \\[3ex] V = \pi r^2 h $
(22.)Two matrices are confirmable for addition if they are of

A. The same order
B. The different order
C. The order 2 × 2
D. The order 3 × 3


Two matrices are confirmable for addition if they are of the same order.
(23.) Distance formula between two points is:

$ A.\;\; \sqrt{(x_2 - x_1)^2 - (y_2 - y_1)^2} \\[3ex] B.\;\; \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \\[3ex] C.\;\; \sqrt{(x_2 + x_1)^2 - (y_2 + y_1)^2} \\[3ex] D.\;\; \sqrt{(x_2 + x_1)^2 + (y_2 - y_1)^2} \\[3ex] $

The distance formula between two points is: $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
(24.) A straight angle contains:

$ A.\;\; 90^\circ \\[3ex] B.\;\; 180^\circ \\[3ex] C.\;\; 270^\circ \\[3ex] D.\;\; 360^\circ \\[3ex] $

A straight angle is an angle of 180°
(25.) Points which do not lie on the same straight line called:

A. Non collinear
B. Collinear
C. Equal
D. Zero


Collinear points are points that lie on the same straight line.
Non-collinear points are points which do not lie on the same straight line.
(26.) The angle bisectors of a triangle are:

A. Concurrent
B. Collinear
C. Perpendicular
D. Non-concurrent


The angle bisectors of a triangle are concurrent.
(27.) If $x^2 = a$, then $x = $?

$ A.\;\; a \\[3ex] B.\;\; \pm a \\[3ex] C.\;\; \sqrt{a} \\[3ex] D.\;\; \pm \sqrt{a} \\[3ex] $

$ x^2 = a \\[3ex] x = \pm \sqrt{a} $
(28.) A line joining one vertex of a triangle to the mid point of its opposite sides is called:

A. Angle bisector
B. Altitude
C. Median
D. Side bisector


The median is the line joining one vertex of a triangle to the mid point of its opposite sides.
(29.) $(a - b)(a^2 + ab + b^2)$ = ?

$ A.\;\; (a - b)^3 \\[3ex] B.\;\; (a + b)^3 \\[3ex] C.\;\; a^3 - b^3 \\[3ex] D.\;\; a^3 + b^3 \\[3ex] $

$ (a - b)(a^2 + ab + b^2) \\[3ex] a(a^2) = a^3 \\[3ex] a(ab) = a^2b \\[3ex] a(b^2) = ab^2 \\[3ex] -b(a^2) = -a^2b \\[3ex] -b(ab) = -ab^2 \\[3ex] -b(b^2) = -b^3 \\[3ex] \implies \\[3ex] a^3 - b^3 $
(30.) Area of a square with side 'S' is

$ A.\;\; S \\[3ex] B.\;\; 4S \\[3ex] C.\;\; 2S \\[3ex] D.\;\; S^2 \\[3ex] $

Area of a square with side 'S' = S²
(31.) Factorization of $a^4 - 1$ is:

$ A.\;\; (a - 1)(a + 1)(a^2 + 1) \\[3ex] B.\;\; (a - 1)(a^2 + 1) \\[3ex] C.\;\; (a + 1)(a^2 - 1) \\[3ex] D.\;\; (a^2 + 1)(a + 1) \\[3ex] $

$ a^4 - 1 \\[4ex] = (a^2)^2 - 1^2 \\[4ex] = (a^2 + 1)(a^2 - 1)...\text{Difference of Two Squares} \\[4ex] ..............................................\\[3ex] a^2 - 1 \\[3ex] = a^2 - 1^2 \\[3ex] = (a + 1)(a - 1) ...\text{Difference of Two Squares} \\[3ex] ..............................................\\[3ex] = (a^2 + 1)(a + 1)(a - 1) $
(32.) A point in a Cartesian plane determines a unique ordered pair of:

A. Set
B. Abscissa
C. Numbers
D. Ordinate


A point in a Cartesian plane determines a unique ordered pair of: Numbers.
The first number is the x-coordinate or abscissa
The second number is the y-coordinate of ordinate.
(33.) Solution of $x + 3 \lt 7$ is:

$ A.\;\; x \gt 4 \\[3ex] B.\;\; x \lt 4 \\[3ex] C.\;\; x \gt -4 \\[3ex] D.\;\; x \lt -4 \\[3ex] $

$ x + 3 \lt 7 \\[3ex] x \lt 7 - 3 \\[3ex] x \lt 4 \\[3ex] $ Check
$x \lt 4; \hspace{3em}Let\;\; x = 3$
LHS RHS
$ x + 3 \\[3ex] 3 + 3 \\[3ex] 6 $ $7$
$6 \lt 7$
(34.) A quadratic equation has a degree:

A. 2
B. 1
C. 0
D. 3


A quadratic equation has a degree: 2
(35.) An equation that can be written in the form $ax + b = 0, \;\;\;a \ne 0$ is called:

A. Linear equation
B. Inequality
C. Solution
D. Constant


A Linear Equation is an equation that can be written as $ax + b = 0, \;\;\;a \ne 0$
(36.) Any value of the variable which makes the equation a true statement is called the .......

A. Equation
B. Inequality
C. Solution
D. Constant


Any value of the variable which makes the equation a true statement is called the solution of the equation.
(37.) The number of altitudes in triangle are:

$ A.\;\; 1 \\[3ex] B.\;\; 2 \\[3ex] C.\;\; 3 \\[3ex] D.\;\; 4 \\[3ex] $

A triangle has three altitudes.
Each altitude is from each vertex, perpendicular to the opposite side.
(38.) An angle containing more than 180° and less than 360° is called:

A. Reflex angle
B. Obtuse angle
C. Straight angle
D. Acute angle


A Reflex angle is an angle containing more than 180° and less than 360°.




Top




(1.)


(2.)


(3.)


(4.)


(5.)


(6.)


(7.)


(8.)


(9.)


(10.)


(11.)


(12.)


(13.)


(14.)


(15.)


(16.)


(17.)


(18.)


(19.)


(20.)


Cash App: Your donation is appreciated. PayPal: Your donation is appreciated. YouTube: Please Subscribe, Share, and Like my Channel
© 2025 Exams Success Group: Your Success in Exams is Our Priority
The Joy of a Teacher is the Success of his Students.