Sequences and Series
Welcome to Our Site
I greet you this day,
These are the solutions to the CSEC past questions on Sequences.
The link to the video solutions will be provided for you. Please
subscribe to the YouTube channel to be notified of upcoming livestreams. You are welcome to ask questions during
the video livestreams.
If you find these resources valuable and helpful in your passing the
Mathematics test of the CSEC, please consider making a donation:
Cash App: $ExamsSuccess or
cash.app/ExamsSuccess
PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess
Google charges me for the hosting of this website and my other
educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well.
As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.
Comments, ideas, areas of improvement, questions, and constructive
criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.
Notable Notes
(1.) If you notice that the pattern represents an arithmetic sequence, it is recommended that you save time by
using the formulas for Arithmetic Sequences
to determine the nth term as applicable.
(2.) If you notice that the pattern represents a geometric sequence, it is recommended that you save time by
using the formulas for Geometric Sequences
to determine the nth term as applicable.
(3.) If the sequence is neither an arithmetic nor a geometric sequence, then it is important to establish a
pattern/rule for each row and column so that we can determine the formula that works
for n
Formula Sheet: List of Formulae
-
Symbols and Formulas: Arithmetic Sequence
- $AS_n$ = $nth$ term of an Arithmetic Sequence
- $a$ = first term
- $p$ = last term
- $d$ = common difference
- $n$ = number of terms
- $SAS_n$ = sum of the first $n$ terms of an Arithmetic Sequence
$ (1.)\:\: AS_n = a + d(n - 1) \\[5ex] (2.)\:\: AS_n = vn + w \:\:where\:\: v = d \:\:and\:\: w = a - d \\[5ex] (3.)\:\: p = a + d(n - 1) \\[5ex] (4.)\:\: SAS_n = \dfrac{n}{2}(a + AS_n) \\[7ex] (5.)\:\: SAS_n = \dfrac{n}{2}(a + p) \\[7ex] (6.)\:\: SAS_n = \dfrac{n}{2}[2a + d(n - 1)] \\[7ex] (7.)\:\: n = \dfrac{2 * SAS_n}{a + p} \\[7ex] (8.)\:\: n = \dfrac{p - a + d}{d} \\[7ex] (9.)\:\: n = \dfrac{-(2a - d) \pm \sqrt{(2a - d)^2 + 8d*SAS_n}}{2d} \\[7ex] (10.)\;\; d = \dfrac{(p - a)(p + a)}{2 * SAS_n - p - a} $
-
Symbols and Formulas: Geometric Sequence
- $GS_n$ = $nth$ term of a Geometric Sequence
- $a$ = first term
- $p$ = last term
- $r$ = common ratio
- $n$ = number of terms
- $SGS_n$ = sum of the first $n$ terms of a Geometric Sequence
- $S_{\infty}$ = sum to infinity of a Geometric Sequence
$ (1.)\:\: GS_n = ar^{n - 1} \\[5ex] (2.)\:\: SGS_n = \dfrac{a(r^{n} - 1)}{r - 1} \:\:for\:\: r \gt 1 \\[7ex] (3.)\:\: SGS_n = \dfrac{a(1 - r^{n})}{1 - r} \:\:for\:\: r \lt 1 \\[7ex] (4.)\:\: n = \dfrac{\log{\left[\dfrac{SGS_n(r - 1)}{a} + 1\right]}}{\log r} \\[7ex] (5.)\:\: If\:\:r \lt 1,\:\:the\:\:series\:\:converges\:\:and\:\: S_{\infty} = \dfrac{a}{1 - r} \\[7ex] (6.)\:\: If\:\:r \gt 1,\:\:the\:\:series\:\:diverges \\[5ex] (7.)\:\: If\:\:r = 1,\:\:S_{\infty}\:\:DNE \\[5ex] (8.)\:\: r = \dfrac{S_{\infty} - a}{S_{\infty}} \\[7ex] (9.)\:\: a = S_{\infty}(1 - r) $
-
Symbols and Formulas: Quadratic Sequence
- $QS_n$ = $n$th term of a Quadratic Sequence = $an^2 + bn + c$
- $1st$ = first term
- $2nd$ = second term
- $3rd$ = third term
- $4th$ = fourth term
- $n$ = number of terms
- $a$ = coefficient of $n^2$
- $b$ = coefficient of $n$
$ QS = 1st,\:\:\:\:2nd,\:\:\:3rd,\:\:\:4th,... \\[5ex] QS_n = an^2 + bn + c \\[5ex] (1.)\:\: a = \dfrac{1st + 3rd - 2(2nd)}{2} \\[7ex] (2.)\:\: b = \dfrac{8(2nd) - 5(1st) - 3(3rd)}{2} \\[7ex] (3.)\:\: c = 3(1st) - 3(2nd) + 3rd \\[5ex] (4.)\:\: \therefore QS_n = \dfrac{1st + 3rd - 2(2nd)}{2} * n^2 + \dfrac{8(2nd) - 5(1st) - 3(3rd)}{2} * n + 3(1st) - 3(2nd) + 3rd \\[7ex] The\:\:Left\:\:Hand\:\:Side\:\:must\;\;be\:\:equal\:\:to\;\;the\:\:Right\:\:Hand\:\:Side \\[5ex] (5.)\:\: a + b + c = 1st \\[5ex] (6.)\:\: 4a + 2b + c = 2nd \\[5ex] (7.)\:\: 9a + 3b + c = 3rd \\[5ex] (8.)\:\: 3a + b = 2nd - 1st \\[5ex] (9.)\:\: 8a + 2b = 3rd - 1st $
-
Symbols and Formulas: Other Sequences
- $TS_n$ = $nth$ term of a Triangular Number Sequence
- $SS_{n}$ = $nth$ term of a Square Number Sequence
- $CS_{n}$ = $nth$ term of a Cube Number Sequence
- $n$ = number of terms
- $STS_n$ = sum of the first $n$ terms of a Triangular Number Sequence
- $SSS_n$ = sum of the first $n$ terms of a Square Number Sequence
- $SCS_n$ = sum of the first $n$ terms of a Cube Number Sequence
$ \underline{Triangular\;\;Number\;\;Sequence} \\[3ex] (1.)\:\: TS_n = \dfrac{n(n + 1)}{2} \\[7ex] (2.)\;\; n = \dfrac{\sqrt{8 * TS_n + 1} - 1}{2} \\[7ex] (3.)\:\: TS_n = C(n + 1, 2)...Combinatorics\;\;symbol\;\;for\;\;Combinations \\[5ex] (4.)\;\; STS_n = \dfrac{n(n + 1)(n + 2)}{6} \\[7ex] (5.)\:\: STS_n = C(n + 2, 3)...Combinatorics\;\;symbol\;\;for\;\;Combinations \\[7ex] \underline{Square\;\;Number\;\;Sequence} \\[3ex] (1.)\:\: SS_n = n^2 \\[5ex] (2.)\;\; n = \sqrt{SS_n} \\[5ex] (3.)\;\; SSS_n = \dfrac{n(n + 1)(2n + 1)}{6} \\[7ex] \underline{Cube\;\;Number\;\;Sequence} \\[3ex] (1.)\:\: CS_n = n^3 \\[5ex] (2.)\;\; n = \sqrt[3]{CS_n} \\[5ex] (3.)\;\; SCS_n = \left[\dfrac{n(n + 1)}{2}\right]^2 \\[7ex] (4.)\;\; n = \dfrac{\sqrt{8\sqrt{SCS_n} + 1} - 1}{2} \\[7ex] $
-
Symbols and Formulas: Recursive Sequence
- $RS_n$ = $nth$ term of a Recursive Sequence
- $RS_{n + 1}$ = next term of a Recursive Sequence
- $a$ = first term (constant)
- $r$ = common ratio (coefficient of the $nth$ term)
- $RS_1$ = initial term
- $n$ = number of terms
- $SRS_n$ = sum of the first $n$ terms of a Recursive Sequence
- $\phi$ = Golden Ratio
- $FS_n$ = $nth$ term of a Fibonacci Sequence
- $SFS_n$ = sum of the first $n$ terms of a Fibonacci Sequence
$ \underline{First-Order\;\;Linear\;\;Recurrence\;\;Relation} \\[3ex] (1.)\:\: RS_{n + 1} = r * RS_{n} + a \\[5ex] (2.)\:\: RS_{n + 1} = \dfrac{RS_1 * r^n(r - 1) + a(r^n - 1)}{r - 1} \;\;\;for\;\;r \gt 1 \\[7ex] (3.)\;\; RS_{n + 1} = \dfrac{RS_1 * r^n(1 - r) + a(1 - r^n)}{1 - r} \;\;\;for\;\;r \lt 1 \\[7ex] \underline{Fibonacci\;\;Sequence} \\[3ex] (1.)\;\; \phi = \dfrac{1 + \sqrt{5}}{2} \\[7ex] (2.)\;\; FS_n = \dfrac{\sqrt{5}}{5}\left[\left(\dfrac{1 + \sqrt{5}}{2}\right)^n - \left(\dfrac{1 - \sqrt{5}}{2}\right)^n\right] \\[7ex] (3.)\;\; FS_n = \dfrac{\sqrt{5}}{5}\left[\phi^n - \left(\dfrac{1 - \sqrt{5}}{2}\right)^n\right] \\[7ex] (4.)\;\; SFS_n = \dfrac{\sqrt{5}}{5}\left[\dfrac{\phi^3(\phi^{n - 1} - 1) + [(\phi - 1)(1 - \phi^2)][(1 - \phi)^{n - 1} - 1]}{\phi(\phi - 1)}\right] + 1 $
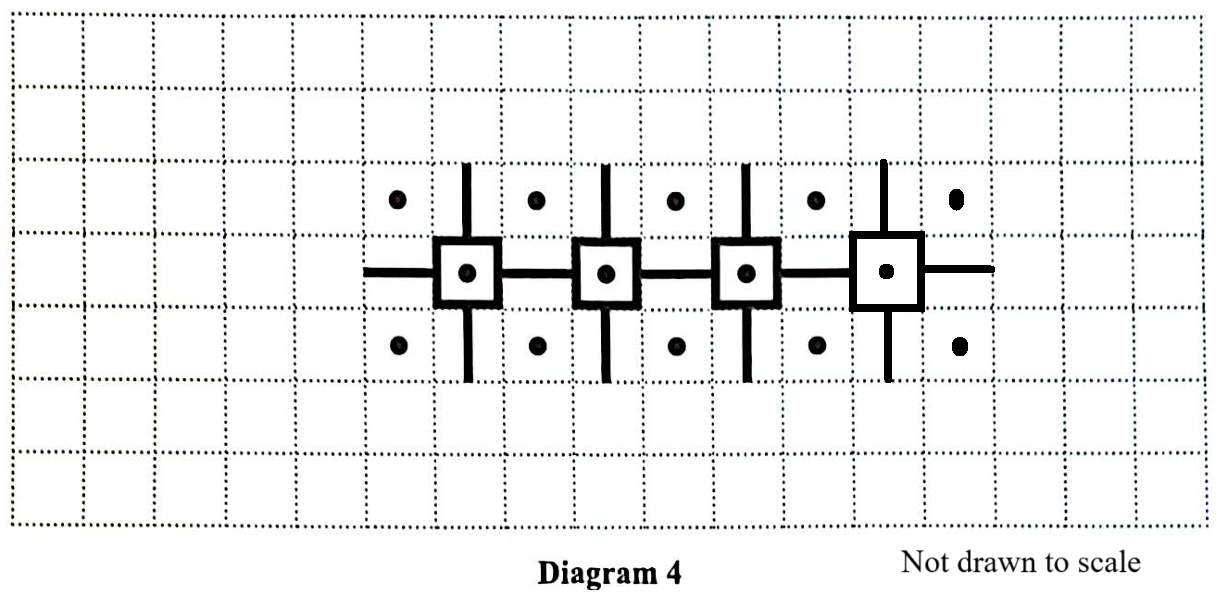
Some of these lines form squares.
The first three diagrams in the sequence are shown below.

(a.) Add more lines and dots to the diagram below to show Diagram 4 of the sequence.

(b.) The number of dots, D, and the number of unit lines that form each diagram, L, form a pattern.
The values for D and L for the first 3 diagrams are written in the table below.
Study the pattern of numbers in each row of the table.
Complete the rows numbered (i.), (ii.), and (iii.)
| Diagram | Number of Dots (D) | Number of Lines (L) |
|---|---|---|
| 1 | 5 | 8 |
| 2 | 8 | 15 |
| 3 | 11 | 22 |
| 4 | ....... | ....... |
| ....... | 59 | ....... |
| n | ....... | ....... |
(c.) One of the diagrams in the sequence has 148 lines.
Calculate the number of dots in this diagram.
(a.) Diagram 4 is:
$ a = \text{first term} \\[3ex] d = \text{common difference} \\[3ex] n = \text{number of terms} \\[5ex] (iii.) \\[3ex] \underline{\text{Number of Dots, D}} \\[3ex] 5, 8, 11, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 5 \\[3ex] d = 8 - 5 = 3 \\[3ex] D_n = a + d(n - 1) \\[3ex] = 5 + 3(n - 1) \\[3ex] = 5 + 3n - 3 \\[3ex] = 3n + 2 \\[3ex] nth\;\;term = 3n + 2 \\[5ex] \underline{\text{Number of Lines, L}} \\[3ex] 8, 15, 22, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 8 \\[3ex] d = 15 - 8 = 7 \\[3ex] L_n = a + d(n - 1) \\[3ex] = 8 + 7(n - 1) \\[3ex] = 8 + 7n - 7 \\[3ex] = 7n + 1 \\[3ex] nth\;\;term = 7n + 1 \\[5ex] (i.) \\[3ex] \underline{\text{4th Diagram}} \\[3ex] n = 4 \\[3ex] D_4 = 3(4) + 2 \\[3ex] = 12 + 2 \\[3ex] = 14 \\[3ex] L_4 = 7(4) + 1 \\[3ex] = 28 + 1 \\[3ex] = 29 \\[5ex] (ii.) \\[3ex] \text{Number of Dots} = 59 \\[3ex] \implies \\[3ex] D_n = 59 \\[3ex] 3n + 2 = 59 \\[3ex] 3n = 59 - 2 \\[3ex] 3n = 57 \\[3ex] n = \dfrac{57}{3} \\[5ex] n = 19...\text{19th Diagram} \\[3ex] L_{19} = 7(19) + 1 \\[4ex] = 133 + 1 \\[3ex] = 134 \\[3ex] $ The completed table is:
| Diagram | Number of Dots (D) | Number of Lines (L) |
|---|---|---|
| 1 | 5 | 8 |
| 2 | 8 | 15 |
| 3 | 11 | 22 |
| 4 | 14 | 29 |
| 19 | 59 | 134 |
| n | 3n + 2 | 7n + 1 |
$ (c.) \\[3ex] L_n = 148 \\[3ex] 7n + 1 = 148 \\[3ex] 7n = 148 - 1 \\[3ex] 7n = 147 \\[3ex] n = \dfrac{147}{7} \\[5ex] n = 21 \\[5ex] D_n = 3(21) + 2 \\[3ex] = 63 + 2 \\[3ex] = 65\;dots $
Each regular hexagon is made using sticks of unit length.
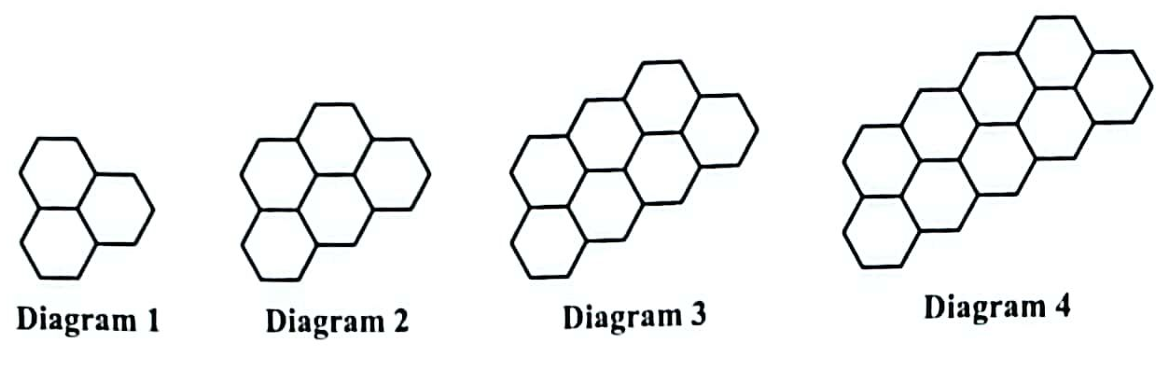
(a.) Complete the diagram below to represent Diagram 5 in the sequence of regular hexagons.
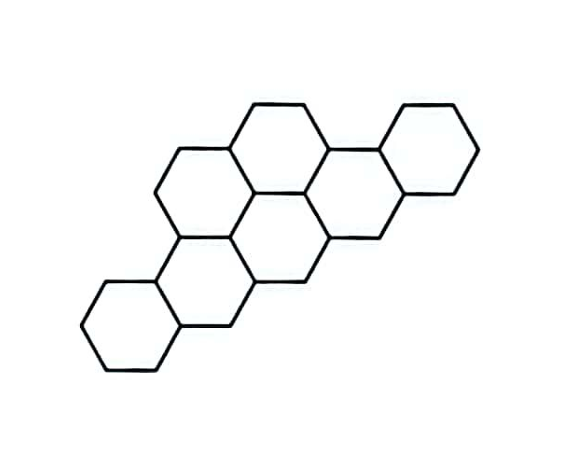
(b.) The number of regular hexagons, H, the number of sticks, S, and the perimeter of each figure, P, follow a pattern.
The values for H, S and P, for the first 4 diagrams are shown in the table below.
Study the pattern of numbers in each row of the table and answer the questions that follow.
Complete the rows marked (i.), (ii.), and (iii.) in the table below.
| Diagram Number (D) | Number of Hexagons (H) | Number of Sticks (S) | Perimeter (P) |
|---|---|---|---|
| 1 | 3 | 15 | 12 |
| 2 | 5 | 23 | 16 |
| 3 | 7 | 31 | 20 |
| 4 | 9 | 39 | 24 |
| 5 | ....... | ....... | 28 |
| ....... | 47 | 191 | ....... |
| n | ....... | ....... | ....... |
(c.) Skyla says that she can make one of these figures with a perimeter of EXACTLY 1005.
Explain why she is incorrect.
(a.) Diagram 5 in the sequence of regular hexagons (Not drawn to scale) is:
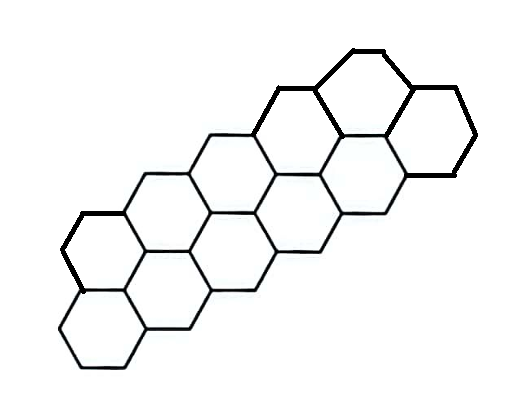
$ a = \text{first term} \\[3ex] d = \text{common difference} \\[3ex] n = \text{number of terms} \\[5ex] (iii.) \\[3ex] \underline{\text{Number of Hexagons, H}} \\[3ex] 3, 5, 7, 9, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 3 \\[3ex] d = 9 - 7 = 7 - 5 = 5 - 3 = 2 \\[3ex] H_n = a + d(n - 1) \\[3ex] = 3 + 2(n - 1) \\[3ex] = 3 + 2n - 2 \\[3ex] = 2n + 1 \\[3ex] nth\;\;term = 2n + 1 \\[5ex] \underline{\text{Number of Sticks, S}} \\[3ex] 15, 23, 31, 39, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 15 \\[3ex] d = 39 - 31 = 31 - 23 = 23 - 15 = 8 \\[3ex] S_n = a + d(n - 1) \\[3ex] = 15 + 8(n - 1) \\[3ex] = 15 + 8n - 8 \\[3ex] = 8n + 7 \\[3ex] nth\;\;term = 8n + 7 \\[5ex] \underline{\text{Perimeter, P}} \\[3ex] 12, 16, 20, 24, 28, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 12 \\[3ex] d = 28 - 24 = 24 - 20 = 20 - 16 = 16 - 12 = 4 \\[3ex] P_n = a + d(n - 1) \\[3ex] = 12 + 4(n - 1) \\[3ex] = 12 + 4n - 4 \\[3ex] = 4n + 8 \\[3ex] nth\;\;term = 4n + 8 \\[5ex] (i.) \\[3ex] \underline{\text{Diagram Number 5}} \\[3ex] n = 5 \\[3ex] H_5 = 2(5) + 1 \\[3ex] = 10 + 1 \\[3ex] = 11 \\[3ex] S_5 = 8(5) + 7 \\[3ex] = 40 + 7 \\[3ex] = 47 \\[5ex] (ii.) \\[3ex] \text{Number of Hexagons} = 47 \\[3ex] \implies \\[3ex] H_n = 47 \\[3ex] 2n + 1 = 47 \\[3ex] 2n = 47 - 1 \\[3ex] 2n = 46 \\[3ex] n = \dfrac{46}{2} \\[5ex] n = 23...\text{Diagram Number 23} \\[3ex] P_{23} = 4(23) + 8 \\[4ex] = 92 + 8 \\[3ex] = 100 \\[3ex] $ The completed table is:
| Diagram Number (D) | Number of Hexagons (H) | Number of Sticks (S) | Perimeter (P) |
|---|---|---|---|
| 1 | 3 | 15 | 12 |
| 2 | 5 | 23 | 16 |
| 3 | 7 | 31 | 20 |
| 4 | 9 | 39 | 24 |
| 5 | 11 | 47 | 28 |
| 23 | 47 | 191 | 100 |
| n | 2n + 1 | 8n + 7 | 4n + 8 |
$ (c.) \\[3ex] P_n = 1005 \\[4ex] 4n + 8 = 1005 \\[3ex] 4n = 1005 - 8 \\[3ex] 4n = 997 \\[3ex] n = \dfrac{997}{4} \\[5ex] n = 249.25 \\[3ex] $ n = 249.25 (which gives a perimeter of 1005) is not a whole number.
Hence, the perimeter of exactly 1005 is not feasible.
Each figure is made using a set of small squares of unit length that are both coloured (shaded) and white (unshaded).
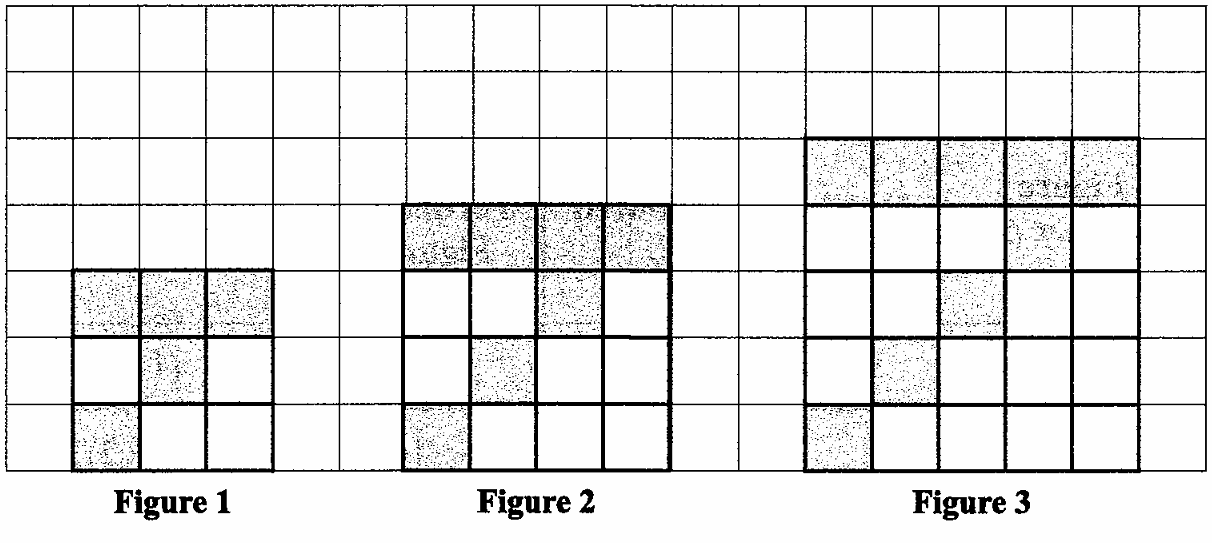
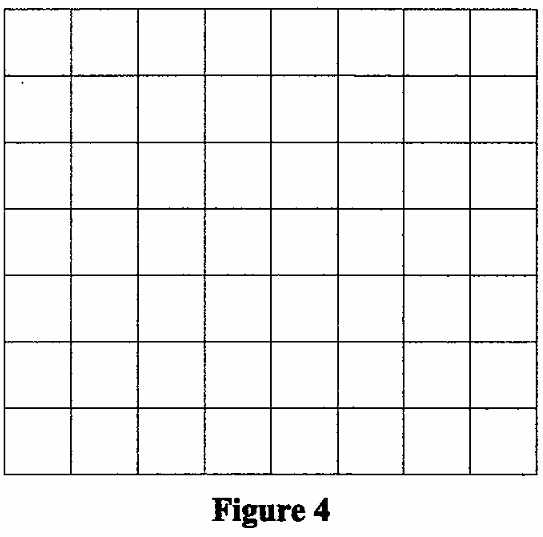
(a.) In the space provided below, draw Figure 4 of the sequence.
(b.) The number of coloured squares, C, the total number of squares, T and the perimeter of the figure, P, follow a pattern.
Study the patterns in the table below and answer the questions that follow.
Complete Rows (i.), (ii.), and (iii) in the table below.
| Figure Number (F) | Number of Coloured Squares (C) | Perimeter of Figure (P) | Total Number of Squares (F) |
|---|---|---|---|
| 1 | 5 | 12 | (1 + 2)² = 9 |
| 2 | 7 | 16 | (2 + 2)² = 16 |
| 3 | 9 | 20 | (3 + 2)² = 25 |
| 11 | ....... | 52 | ....... |
| ....... | 49 | ....... | (23 + 2)² = 625 |
| n | ....... | ....... | ....... |
(c.) How many white squares are in Figure 11.?
(a.) Figure 4 of the sequence is drawn as shown:

$ a = \text{first term} \\[3ex] d = \text{common difference} \\[3ex] n = \text{number of terms} \\[5ex] (iii.) \\[3ex] \underline{\text{Number of Coloured Squares, C}} \\[3ex] 5, 7, 9, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 5 \\[3ex] d = 7 - 5 = 2 \\[3ex] C_n = a + d(n - 1) \\[3ex] = 5 + 2(n - 1) \\[3ex] = 5 + 2n - 2 \\[3ex] = 2n + 3 \\[3ex] nth\;\;term = 2n + 3 \\[5ex] \underline{\text{Perimeter of Figure, P}} \\[3ex] 12, 16, 20, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 12 \\[3ex] d = 16 - 12 = 4 \\[3ex] P_n = a + d(n - 1) \\[3ex] = 12 + 4(n - 1) \\[3ex] = 12 + 4n - 4 \\[3ex] = 4n + 8 \\[3ex] = 4(n + 2) \\[3ex] nth\;\;term = 4(n + 2) \\[5ex] (i.) \\[3ex] \underline{\text{11th Figure}} \\[3ex] n = 11 \\[3ex] C_{11} = 2(11) + 3 \\[3ex] = 22 + 3 \\[3ex] = 25 \\[3ex] \text{Total Number of Squares is not an Arithmetic Sequence} \\[3ex] \text{We shall find it another way} \\[5ex] (ii.) \\[3ex] \text{Number of Coloured Squares} = 49 \\[3ex] \implies \\[3ex] C_n = 49 \\[3ex] 2n + 3 = 49 \\[3ex] 2n = 49 - 3 \\[3ex] 2n = 46 \\[3ex] n = \dfrac{46}{2} \\[5ex] n = 23...\text{23rd Figure} \\[3ex] P_{23} = 4(n + 2) \\[4ex] = 4(23 + 2) \\[3ex] = 4(25) \\[3ex] = 100 \\[3ex] $ (b.) We shall use the dark blue color to see the patterns.
| Figure Number (F) | Number of Coloured Squares (C) | Perimeter of Figure (P) | Total Number of Squares (F) |
|---|---|---|---|
| $\color{darkblue}{1}$ | $5 = \color{darkblue}{1}(2) + 3$ | $12 = 4(\color{darkblue}{1} + 2)$ | $(\color{darkblue}{1} + 2)^2 = 9$ |
| $\color{darkblue}{2}$ | $7 = \color{darkblue}{2}(2) + 3$ | $16 = 4(\color{darkblue}{2} + 2)$ | $(\color{darkblue}{2} + 2)^2 = 16$ |
| $\color{darkblue}{3}$ | $9 = \color{darkblue}{3}(2) + 3$ | $20 = 4(\color{darkblue}{3} + 2)$ | $(\color{darkblue}{3} + 2)^2 = 25$ |
| $\color{darkblue}{11}$ | $\color{darkblue}{11}(2) + 3 = 25$ | $4(\color{darkblue}{11} + 2) = 52$ | $(\color{darkblue}{11} + 2)^2 = 169$ |
| $\color{darkblue}{23}$ | $\color{darkblue}{23}(2) + 3 = 49$ | $4(\color{darkblue}{23} + 2) = 100$ | $(\color{darkblue}{23} + 2)^2 = 625$ |
| $\color{darkblue}{n}$ | $\color{darkblue}{n}(2) + 3 = 2n + 3$ | $4(\color{darkblue}{n} + 2) = 4(n + 2)$ | $(\color{darkblue}{n} + 2)^2 = (n + 2)^2$ |
(c.) The sum of the number of coloured squares and the number of white squares is the total number of squares
Number of white squares = Total number of squares − Number of coloured squares
For Figure 11:
Number of white squares = 169 − 25 = 144.
The first 3 designs in the sequence are shown below.
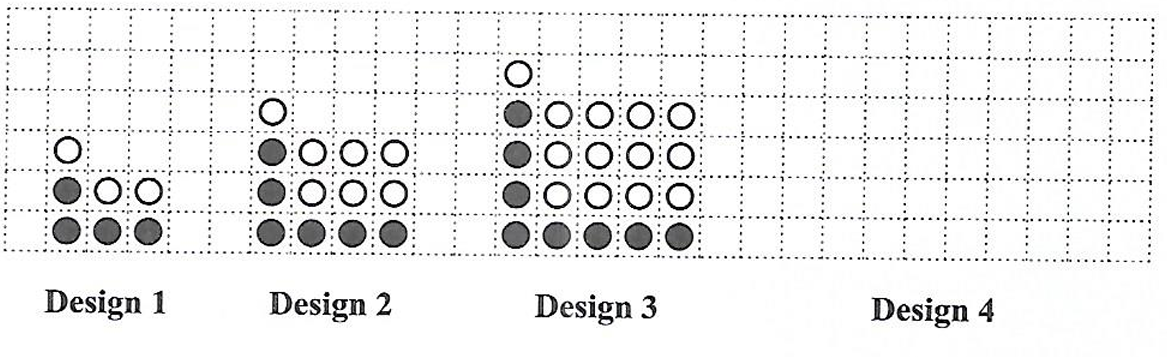
(a.) In the space provided on the grid above, draw Design 4.
(b.) The number of white discs, W, the number of black discs, B, and the total number of discs, T, that form each design follows a pattern.
The values for W, B and T for the first 3 designs are shown in the table below.
Study the pattern of numbers in the table.
Complete Rows (i), (ii), and (iii.) in the table below.
| Design Number (P) | Number of White Discs (W) | Number of Black Discs (B) | Total Number of Discs (T) |
|---|---|---|---|
| 1 | (1 × 1) + 1 + 1 = 3 | 4 | 7 |
| 2 | (2 × 2) + 2 + 1 = 7 | 6 | 13 |
| 3 | (3 × 3) + 3 + 1 = 13 | 8 | 21 |
| 9 | (....... × .......) + ....... + ....... = ....... | ....... | 111 |
| ....... | (20 × 20) + 20 + 1 = 421 | ....... | ....... |
| n | ....... | ....... | ....... |
(c.) Stephen has 28 black discs and 154 white discs, and wants to make Design 12.
Explain why it is NOT possible for him to make Design 12.
(a.) Design 4 of the sequence is drawn as shown:

$ (b.)(i.)\;\;and\;\;(iii.) \\[3ex] \underline{\text{Number of White Discs, W}} \\[3ex] For\;\;n = 9 \\[3ex] W_9 = (9 * 9) + 9 + 1 \\[3ex] W_9 = 91 \\[5ex] For\;\; n = n \\[3ex] nth\;\;term = W_n = (n * n) + n + 1 \\[3ex] W_n = n^2 + n + 1 \\[5ex] \underline{\text{Number of Black Discs, B}} \\[3ex] a = \text{first term} \\[3ex] d = \text{common difference} \\[3ex] n = \text{number of terms} \\[5ex] 4, 6, 8, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 4 \\[3ex] d = 8 - 6 = 6 - 4 = 2 \\[3ex] B_n = a + d(n - 1) \\[3ex] = 4 + 2(n - 1) \\[3ex] = 4 + 2n - 2 \\[3ex] = 2n + 2 \\[3ex] nth\;\;term = B_n = 2n + 2 \\[5ex] For\;\;n = 9 \\[3ex] B_9 = 2(9) + 2 \\[3ex] = 18 + 2 \\[5ex] \underline{\text{Total Number of Discs, T}} \\[3ex] For\;\;n = 9 \\[3ex] T_9 = W_9 + B_9 \\[3ex] = 91 + 20 \\[3ex] = 111 \\[5ex] For\;\; n = n \\[3ex] T_n = W_n + B_n \\[3ex] = n^2 + n + 1 + 2n + 2 \\[3ex] = n^2 + 3n + 3 \\[3ex] nth\;\;term = T_n = n^2 + 3n + 3 \\[5ex] (ii.) \\[3ex] W_n = (20 * 20) + 20 + 1 = 421 \implies n = 20 \\[5ex] B_{20} = 2(20) + 2 \\[3ex] = 40 + 2 \\[3ex] = 42 \\[5ex] T_{20} = W_{20} + B_{20} \\[3ex] = 421 + 42 \\[3ex] = 463 \\[5ex] $ Let us complete the table.
We shall use the dark blue color to see the pattern.
| Design Number (P) | Number of White Discs (W) | Number of Black Discs (B) | Total Number of Discs (T) |
|---|---|---|---|
| $\color{darkblue}{1}$ | $(\color{darkblue}{1} \times \color{darkblue}{1}) + \color{darkblue}{1} + 1 = 3$ | $4 = 2(\color{darkblue}{1}) + 2$ | $7 = (\color{darkblue}{1})^2 + 3(\color{darkblue}{1}) + 3$ |
| $\color{darkblue}{2}$ | $(\color{darkblue}{2} \times \color{darkblue}{2}) + \color{darkblue}{2} + 1 = 7$ | $6 = 2(\color{darkblue}{2}) + 2$ | $13 = (\color{darkblue}{2})^2 + 3(\color{darkblue}{2}) + 3$ |
| $\color{darkblue}{3}$ | $(\color{darkblue}{3} \times \color{darkblue}{3}) + \color{darkblue}{3} + 1 = 13$ | $8 = 2(\color{darkblue}{3}) + 2$ | $21 = (\color{darkblue}{3})^2 + 3(\color{darkblue}{3}) + 3$ |
| $\color{darkblue}{9}$ | $(\color{darkblue}{9} \times \color{darkblue}{9}) + \color{darkblue}{9} + 1 = 19$ | $20 = 2(\color{darkblue}{9}) + 2$ | $111 = (\color{darkblue}{9})^2 + 3(\color{darkblue}{9}) + 3$ |
| $\color{darkblue}{20}$ | $(\color{darkblue}{20} \times \color{darkblue}{20}) + \color{darkblue}{20} + 1 = 421$ | $42 = 2(\color{darkblue}{20}) + 2$ | $463 = (\color{darkblue}{20})^2 + 3(\color{darkblue}{20}) + 3$ |
| $\color{darkblue}{n}$ | $(\color{darkblue}{n} \times \color{darkblue}{n}) + \color{darkblue}{n} + 1 = n^2 + n + 1$ | $2(\color{darkblue}{n}) + 2$ | $(\color{darkblue}{n})^2 + 3(\color{darkblue}{n}) + 3$ |
$ (c.) \\[3ex] \underline{\text{Design 12}} \\[3ex] n = 12 \\[3ex] W_{12} = 12^2 + 12 + 1 \\[3ex] = 144 + 12 + 1 \\[3ex] = 157 \\[3ex] $ Stephen needs 157 white discs to make Design 12.
But he has 154 white discs.
Hence, it is NOT possible for him to make Design 12.
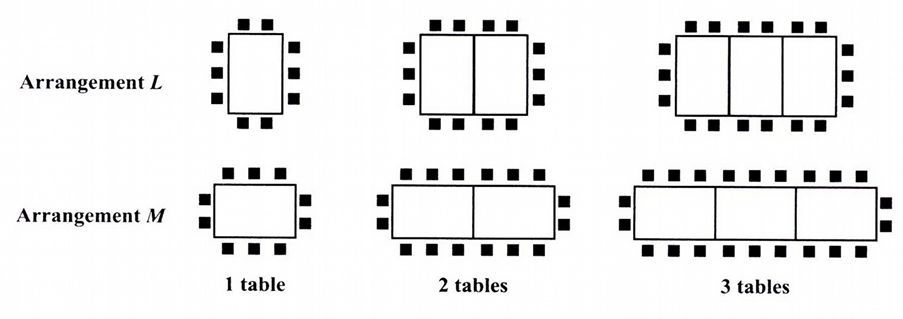
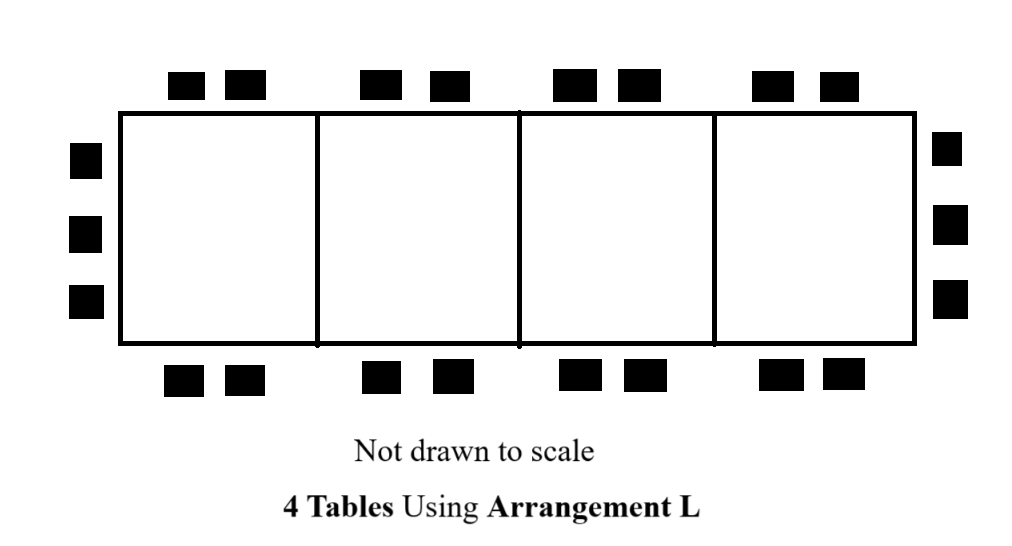
(a.) Draw the diagram for 4 tables using Arrangement L
(b.) The number of chairs, C, that can be placed around a given number of tables, T, for either arrangement, L or M, forms a pattern.
The values for C for the first 3 diagrams for both arrangements are shown in the table below.
Study the pattern of numbers in each row of the table.
Complete the rows numbered (i.), (ii.), and (iii.)
| Number of Tables (T) |
Arrangement L Number of Chairs (C) |
Arrangement M Number of Chairs (C) |
|---|---|---|
| 1 | 10 | 10 |
| 2 | 14 | 16 |
| 3 | 18 | 22 |
| 4 | ....... | ....... |
| ....... | ....... | 130 |
| n | ....... | ....... |
(c.) Leon needs to arrange tables to seat 70 people for a birthday party.
Which of the arrangements, L or M, will allow him to rent the LEAST number of tables?
Use calculations to justify your answer.
(a.) The diagram for 4 tables using Arrangement L is:
$ a = \text{first term} \\[3ex] d = \text{common difference} \\[3ex] n = \text{number of terms} \\[5ex] (iii.) \\[3ex] \underline{\text{Arrangement L: Number of Chairs, LC}} \\[3ex] 10, 14, 18, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 10 \\[3ex] d = 14 - 10 = 4 \\[3ex] LC_n = a + d(n - 1) \\[3ex] = 10 + 4(n - 1) \\[3ex] = 10 + 4n - 4 \\[3ex] = 4n + 6 \\[3ex] nth\;\;term = 4n + 6 \\[5ex] \underline{\text{Arrangement M: Number of Chairs, MC}} \\[3ex] 10, 16, 22, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 10 \\[3ex] d = 16 - 10 = 6 \\[3ex] MC_n = a + d(n - 1) \\[3ex] = 10 + 6(n - 1) \\[3ex] = 10 + 6n - 6 \\[3ex] = 6n + 4 \\[3ex] nth\;\;term = 6n + 4 \\[5ex] (i.) \\[3ex] \underline{\text{4 Tables}} \\[3ex] n = 4 \\[3ex] LC_4 = 4(4) + 6 \\[3ex] = 16 + 6 \\[3ex] = 22 \\[3ex] MC_4 = 6(4) + 4 \\[3ex] = 24 + 4 \\[3ex] = 28 \\[5ex] (ii.) \\[3ex] \text{Arrangement M: Number of Chairs} = 130 \\[3ex] \implies \\[3ex] MC_n = 130 \\[3ex] 6n + 4 = 130 \\[3ex] 6n = 130 - 4 \\[3ex] 6n = 126 \\[3ex] n = \dfrac{126}{6} \\[5ex] n = 21...\text{21 Tables} \\[3ex] LC_{21} = 4(21) + 6 \\[4ex] = 84 + 6 \\[3ex] = 90 \\[3ex] $ (b.) We shall use the dark blue color to see the patterns.
| Number of Tables (T) |
Arrangement L Number of Chairs (C) |
Arrangement M Number of Chairs (C) |
|---|---|---|
| $\color{darkblue}{1}$ | $10 = 2(\color{darkblue}{1} + \color{darkblue}{1}) + 6$ | $10 = 3(\color{darkblue}{1} + \color{darkblue}{1}) + 4$ |
| $\color{darkblue}{2}$ | $14 = 2(\color{darkblue}{2} + \color{darkblue}{2}) + 6$ | $16 = 3(\color{darkblue}{2} + \color{darkblue}{2}) + 4$ |
| $\color{darkblue}{3}$ | $18 = 2(\color{darkblue}{3} + \color{darkblue}{3}) + 6$ | $22 = 3(\color{darkblue}{3} + \color{darkblue}{3}) + 4$ |
| $\color{darkblue}{4}$ | $22 = 2(\color{darkblue}{4} + \color{darkblue}{4}) + 6$ | $28 = 3(\color{darkblue}{4} + \color{darkblue}{4}) + 4$ |
| $\color{darkblue}{21}$ | $90 = 2(\color{darkblue}{21} + \color{darkblue}{21}) + 6$ | $ 3(\color{darkblue}{what} + \color{darkblue}{what}) + 4 = 130 \\[3ex] 3(2what) + 4 = 130 \\[3ex] 6\cdot what + 4 = 130 \\[3ex] 6\cdot what = 130 - 4 \\[3ex] 6\cdot what = 126 \\[3ex] what = \dfrac{126}{6} \\[5ex] what = 21 \\[3ex] \underline{Check} \\[3ex] 130 = 3(\color{darkblue}{21} + \color{darkblue}{21}) + 4 $ |
| $\color{darkblue}{n}$ | $ 2(\color{darkblue}{n} + \color{darkblue}{n}) + 6 \\[3ex] 2(2n) + 6 \\[3ex] 4n + 6 $ | $ 3(\color{darkblue}{n} + \color{darkblue}{n}) + 4 \\[3ex] 3(2n) + 4 \\[3ex] 6n + 4 $ |
(c.) Seating 70 people for a birthday party implies 70 chairs
So, let us determine the least number of tables for 70 chairs
$ \underline{Arrangement\;L} \\[3ex] 4n + 6 = 70 \\[3ex] 4n = 70 - 6 \\[3ex] 4n = 64 \\[3ex] n = \dfrac{64}{4} \\[5ex] n = 16\;tables \\[5ex] \underline{Arrangement\;M} \\[3ex] 6n + 4 = 70 \\[3ex] 6n = 70 - 4 \\[3ex] 6n = 66 \\[3ex] n = \dfrac{66}{6} \\[5ex] n = 11\;tables \\[3ex] $ The calculations show that Arrangement M will allow him to rent the LEAST number of tables for 70 people.
Each shape is made using a set of small white counters and black counters.
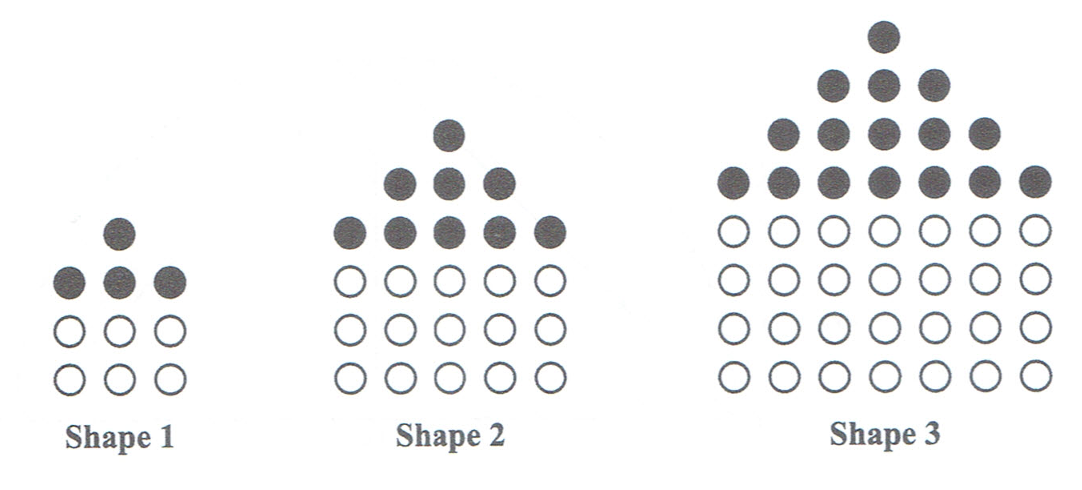
(a.) Complete the diagram below to represent Shape 4.
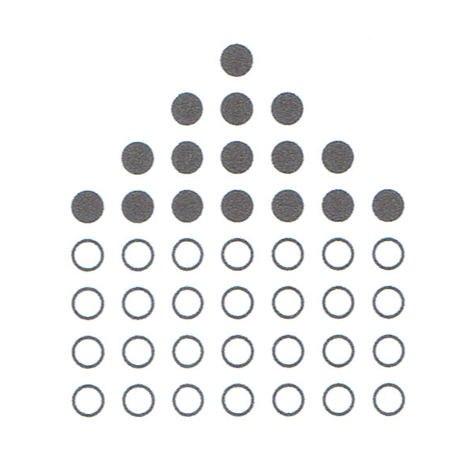
(b.) The number of white counters, W, the number of black counters, B, and the total number of counters, T, that form each shape follow a pattern.
The values for W, B and T for the first 3 shapes are shown in the table below.
Study the pattern of numbers in each row of the table and answer the questions that follow.
Complete the rows marked (i.), (ii.), and (iii.) in the table below.
| Shape Number (S) | Number of White Counters (W) | Number of Black Counters (B) | Total Number of Counters (T) |
|---|---|---|---|
| 1 | (1 + 1)[2(1) + 1] = 6 | (1 + 1)² = 4 | 10 |
| 2 | (2 + 1)[2(2) + 1] = 15 | (2 + 1)² = 9 | 24 |
| 3 | (3 + 1)[2(3) + 1] = 28 | (3 + 1)² = 16 | 44 |
| 4 | 45 | ....... | ....... |
| ....... | ....... | 144 | 420 |
| n | (....... + .......)[....... + .......] | (....... + .......)² | $3n^2 + 5n + 2$ |
(c.) The expression for the total number of counters, $T = W + B$, in Shape S is given by $T = aS^2 + bS + 2$, where a and b are both positive integers.
By substituting suitable values for S, show that the total number of counters in Shape 1 and Shape 3, in terms of a and b, is represented by the equations
$ a + b = 8 \;\;\text{and} \\[3ex] 3a + b = 14 \;\;\text{respectively}. \\[3ex] $
(a.) The diagram that represents Shape 4 is:

(b.) CSEC was so kind to show us the pattern for the Number of White Counters and the Number of Black Counters.
We are going to use that pattern.
We shall use the dark blue color color to see the patterns.
| Shape Number (S) | Number of White Counters (W) | Number of Black Counters (B) | Total Number of Counters (T) |
|---|---|---|---|
| $\color{darkblue}{1}$ | $(\color{darkblue}{1} + 1)[2(\color{darkblue}{1}) + 1] = 6$ | $(\color{darkblue}{1} + 1)^2 = 4$ | 10 |
| $\color{darkblue}{2}$ | $(\color{darkblue}{2} + 1)[2(\color{darkblue}{2}) + 1] = 15$ | $(\color{darkblue}{2} + 1)^2 = 9$ | 24 |
| $\color{darkblue}{3}$ | $(\color{darkblue}{3} + 1)[2(\color{darkblue}{3}) + 1] = 28$ | $(\color{darkblue}{3} + 1)^2 = 16$ | 44 |
| $\color{darkblue}{4}$ | 45 | $(\color{darkblue}{4} + 1)^2 = 5^2 = 25$ | $45 + 25 = 70$ |
| $\color{darkblue}{11}$ | $ W + B = T \\[3ex] W + 144 = 420 \\[3ex] W = 420 - 144 \\[3ex] W = 276 $ |
144 $ (\color{darkblue}{S} + 1)^2 \\[4ex] (S + 1)^2 = 144 \\[4ex] S + 1 = \sqrt{144} \\[3ex] S + 1 = 12 \\[3ex] S = 12 - 1 \\[3ex] S = 11 $ |
420 |
| $\color{darkblue}{n}$ | $ (\color{darkblue}{n} + 1)[2(\color{darkblue}{n}) + 1] \\[3ex] (\color{darkblue}{n} + 1)[2\color{darkblue}{n} + 1] $ | $(\color{darkblue}{n} + 1)^2$ | $3n^2 + 5n + 2$ |
$ (c.) \\[3ex] T = W + B...eqn.(1) \\[3ex] T = aS^2 + bS + 2...eqn.(2) \\[3ex] T = T \\[3ex] \underline{\text{Shape } 1} \\[3ex] S = 1 \\[3ex] T = 10 \\[3ex] \implies \\[3ex] a(1)^2 + b(1) + 2 = 10 \\[3ex] a(1) + b = 10 - 2 \\[3ex] a + b = 8 \\[5ex] \underline{\text{Shape } 3} \\[3ex] S = 3 \\[3ex] T = 44 \\[3ex] \implies \\[3ex] a(3)^2 + b(3) + 2 = 44 \\[3ex] a(9) + 3b = 44 - 2 \\[3ex] 9a + 3b = 42 \\[3ex] 3(3a + b) = 42 \\[3ex] 3a + b = \dfrac{42}{3} \\[5ex] 3a + b = 14 $
The lines form a series of octagons and squares.
The dots are placed at each vertex.
The first 3 figures in the sequence are shown below.
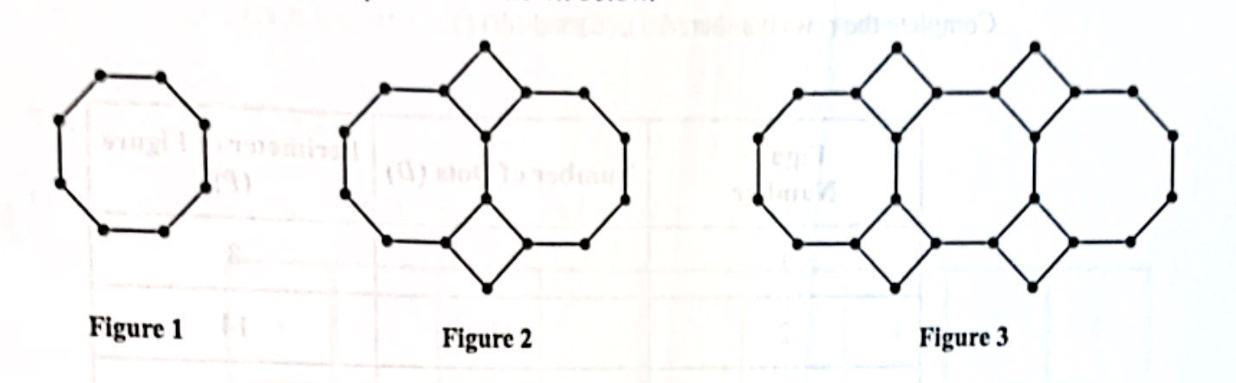
(a.) Figure 3 of the sequence is shown by itself below.
Add more lines of unit length and dots to Figure 3 to correctly represent Figure 4.

(b.) The number of dots, D, and the number of unit lines that form the perimeter of the shape, P, form a pattern.
The values for D and P for the first 3 figures are written in the table below.
Study the pattern of numbers in each row of the table.
Complete the rows numbered (i.), (ii.), and (iii.)
| Figure Number | Number of Dots (D) | Perimeter of Figure (P) |
|---|---|---|
| 1 | 8 | 8 |
| 2 | 16 | 14 |
| 3 | 24 | 20 |
| 4 | ....... | ....... |
| ....... | ....... | 86 |
| n | ....... | ....... |
(c.) For any figure, n > 1, the number of dots, D, is greater than its perimeter, P.
Determine the value of n for a figure in which the difference between D and P is 36.
(a.) Figure 4 of the sequence is drawn as shown:

$ a = \text{first term} \\[3ex] d = \text{common difference} \\[3ex] n = \text{number of terms} = \text{Figure Number} \\[5ex] (iii.) \\[3ex] \underline{\text{Number of Dots, D}} \\[3ex] 8, 16, 24, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 8 \\[3ex] d = 24 - 16 = 16 - 8 = 8 \\[3ex] D_n = a + d(n - 1) \\[3ex] = 8 + 8(n - 1) \\[3ex] = 8 + 8n - 8 \\[3ex] = 8n \\[3ex] nth\;\;term = D_n = 8n \\[5ex] \underline{\text{Perimeter of Figure, P}} \\[3ex] 8, 14, 20, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 8 \\[3ex] d = 20 - 14 = 14 - 8 = 6 \\[3ex] P_n = a + d(n - 1) \\[3ex] = 8 + 6(n - 1) \\[3ex] = 8 + 6n - 6 \\[3ex] = 6n + 2 \\[3ex] nth\;\;term = P_n = 6n + 2 \\[5ex] (i.) \\[3ex] n = 4 \\[3ex] D_4 = 8(4) \\[3ex] = 32 \\[3ex] P_4 = 6(4) + 2 \\[3ex] = 24 + 2 \\[3ex] = 26 \\[5ex] (ii.) \\[3ex] P_n = 86 \\[3ex] \implies \\[3ex] 6n + 2 = 86 \\[3ex] 6n = 86 - 2 \\[3ex] 6n = 84 \\[3ex] n = \dfrac{84}{2} \\[5ex] n = 14 \\[3ex] D_4 = 8(14) \\[3ex] = 112 \\[3ex] $ Let us use the dark blue color to see the patterns in the completed table.
| Figure Number | Number of Dots (D) | Perimeter of Figure (P) |
|---|---|---|
| $\color{darkblue}{1}$ | $8 = 8(\color{darkblue}{1})$ | $8 = 6(\color{darkblue}{1}) + 2$ |
| $\color{darkblue}{2}$ | $16 = 8(\color{darkblue}{2})$ | $14 = 6(\color{darkblue}{2}) + 2$ |
| $\color{darkblue}{3}$ | $24 = 8(\color{darkblue}{3})$ | $20 = 6(\color{darkblue}{3}) + 2$ |
| $\color{darkblue}{4}$ | $32 = 8(\color{darkblue}{4})$ | $26 = 6(\color{darkblue}{4}) + 2$ |
| $\color{darkblue}{14}$ | $112 = 8(\color{darkblue}{14})$ | $86 = 6(\color{darkblue}{14}) + 2$ |
| $\color{darkblue}{n}$ | $8(\color{darkblue}{n})$ | $6(\color{darkblue}{n}) + 2$ |
$ (c.) \\[3ex] D_n - P_n = 36 \\[3ex] 8n - (6n + 2) = 36 \\[3ex] 8n - 6n - 2 = 36 \\[3ex] 2n = 36 + 2 \\[3ex] 2n = 38 \\[3ex] n = \dfrac{38}{2} \\[5ex] n = 19 $

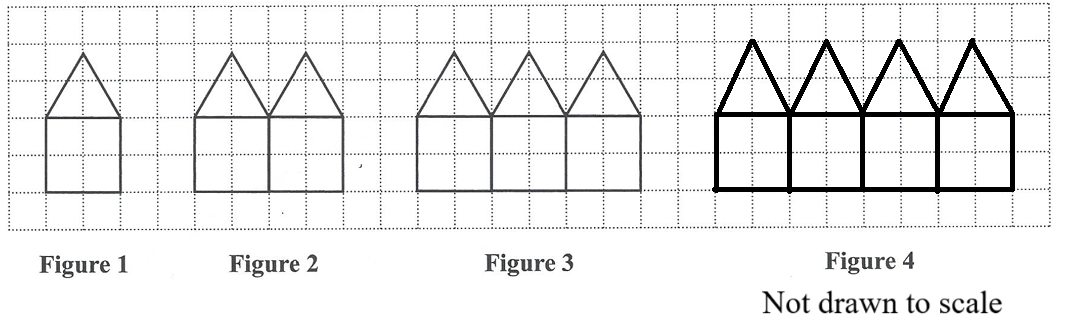
(a.) Draw Figure 4 of the pattern in the space provided above.
(b.) The number of lines, L, in each shape and the perimeter, P, of the shape follow a pattern.
Study the pattern of numbers in each row of the table below and answer the questions that follow.
Complete the table below showing the number of lines and the perimeter of each figure.
| Figure | Number of Lines (L) | Perimeter (P) |
|---|---|---|
| 1 | 6 | 5 |
| 2 | 11 | 8 |
| 3 | 16 | 11 |
| 5 | ....... | ....... |
| ....... | 66 | ....... |
| n | ....... | ....... |
(c.) Write a simplified expression, in terms of n, for the difference, d, between the number of lines and the perimeter of any figure, n.
(a.) Figure 4 of the sequence is drawn as shown:
$ a = \text{first term} \\[3ex] d = \text{common difference} \\[3ex] n = \text{number of terms} = \text{Figure Number} \\[5ex] (iii.) \\[3ex] \underline{\text{Number of Lines, L}} \\[3ex] 6, 11, 16, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 6 \\[3ex] d = 16 - 11 = 11 - 6 = 5 \\[3ex] L_n = a + d(n - 1) \\[3ex] = 6 + 5(n - 1) \\[3ex] = 6 + 5n - 5 \\[3ex] = 5n + 1 \\[3ex] nth\;\;term = L_n = 5n + 1 \\[5ex] \underline{\text{Perimeter, P}} \\[3ex] 5, 8, 11, ... \text{indicates an Arithmetic Sequence} \\[3ex] a = 5 \\[3ex] d = 11 - 8 = 8 - 5 = 3 \\[3ex] P_n = a + d(n - 1) \\[3ex] = 5 + 3(n - 1) \\[3ex] = 5 + 3n - 3 \\[3ex] = 3n + 2 \\[3ex] nth\;\;term = P_n = 3n + 2 \\[5ex] (i.) \\[3ex] n = 5 \\[3ex] L_5 = 5(5) + 1 \\[3ex] = 25 + 1 \\[3ex] = 26 \\[3ex] P_5 = 3(5) + 2 \\[3ex] = 15 + 2 \\[3ex] = 17 \\[5ex] (ii.) \\[3ex] L_n = 66 \\[3ex] \implies \\[3ex] 5n + 1 = 66 \\[3ex] 5n = 66 - 1 \\[3ex] 5n = 65 \\[3ex] n = \dfrac{65}{5} \\[5ex] n = 13 \\[3ex] P_{13} = 3(13) + 2 \\[3ex] = 39 + 2 \\[3ex] = 41 \\[3ex] $ Let us use the dark blue color to see the patterns in the completed table.
| Figure | Number of Lines (L) | Perimeter (P) |
|---|---|---|
| $\color{darkblue}{1}$ | $6 = 5(\color{darkblue}{1}) + 1$ | $5 = 3(\color{darkblue}{1}) + 2$ |
| $\color{darkblue}{2}$ | $11 = 5(\color{darkblue}{2}) + 1$ | $8 = 3(\color{darkblue}{2}) + 2$ |
| $\color{darkblue}{3}$ | $16 = 5(\color{darkblue}{3}) + 1$ | $11 = 3(\color{darkblue}{3}) + 2$ |
| $\color{darkblue}{5}$ | $26 = 5(\color{darkblue}{5}) + 1$ | $17 = 3(\color{darkblue}{5}) + 2$ |
| $\color{darkblue}{13}$ | $66 = 5(\color{darkblue}{13}) + 1$ | $41 = 3(\color{darkblue}{13}) + 2$ |
| $\color{darkblue}{n}$ | $5(\color{darkblue}{n}) + 1$ | $3(\color{darkblue}{n}) + 2$ |
$ (c.) \\[3ex] difference = d \\[3ex] d = L_n - P_n \\[3ex] d = (5n + 1) - (3n + 2) \\[3ex] d = 5n + 1 - 3n - 2 \\[3ex] d = 2n - 1 $
Each figure has one dot at the centre and 4 dots on the circumference of each circle.
The radius of the first circle is one unit.
The radius of each new circle is one unit greater than the radius of the previous circle.
Except for the first figure, a portion of each of the other figures is shaded.
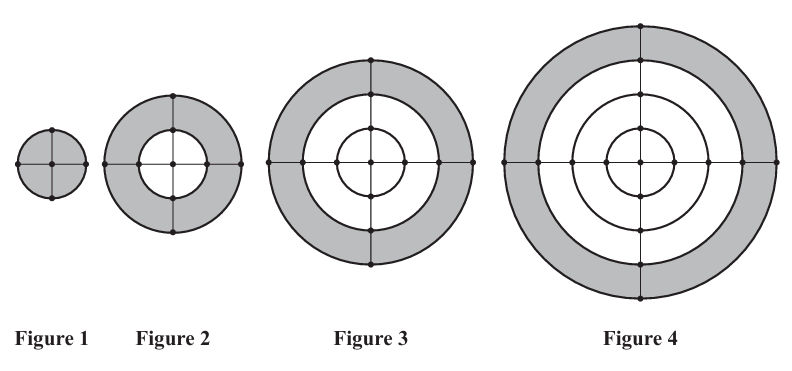
(a.) Complete the rows in the table below for Figure 5 and Figure n
| Figure Number | Number of Dots | Area of Outer (Largest) Circle | Area of Shaded Region | Total Length of Circumference of all Circles |
|---|---|---|---|---|
| 1 | 5 | π | π | 2π |
| 2 | 9 | 4π | 3π | 6π |
| 3 | 13 | 9π | 5π | 12π |
| 4 | 17 | 16π | 7π | 20π |
| 5 | ....... | 25π | ....... | ....... |
| n | ....... | ....... | ....... | ....... |
(b.) Determine the value of n, when the number of dots in Figure n is 541.
(c.) Write down, in terms of p and π, the area of the LARGEST circle in Figure 3p
Let us simplify the information for easier comprehension.
In that sense, we shall introduce more columnns to the table.
The main goal is to establish a pattern/rule for each subsequent row after the first row so that we can determine the formula that works for n
| Figure Number | Number of Dots | Number of Circles | Radii of Circles, r | Area of Outer (Largest) Circle = πr2 | Area of Larger Circle = πr2 | Area of Shaded Region = Area of Largest Circle − Area of Larger Circle (Number of Circles > 1) | Total Length of Circumference of all Circles = 2πr |
|---|---|---|---|---|---|---|---|
| 1 | 5 | 1 | 1 | $ \pi \cdot (1)^2 \\[3ex] \pi $ | $ \pi \cdot (1)^2 \\[3ex] \pi $ | $ \pi \cdot (1)^2 \\[3ex] \pi $ | $ 2\pi(1) \\[3ex] 2\pi $ |
| 2 | $ 5 + 4 = 9 \\[3ex] \implies \\[3ex] 5 + 4(1) \\[3ex] 5 + 4(\color{darkblue}{2} - 1) $ | 2 | 1, 2 | $ \pi \cdot (\color{darkblue}{2})^2 \\[3ex] 4\pi $ | $ \pi \cdot (\color{darkblue}{2} - 1)^2 \\[3ex] \pi \cdot (1)^2 \\[3ex] \pi $ | $ 4\pi - \pi = 3\pi $ | $ 2\pi(1) + 2\pi(2) \\[3ex] 2\pi + 4\pi 6\pi \\[3ex] \implies \\[3ex] \pi \cdot 2 \cdot 3 \\[3ex] \pi \cdot \color{darkblue}{2} \cdot (\color{darkblue}{2} + 1) $ |
| 3 | $ 5 + 4 + 4 = 13 \\[3ex] \implies \\[3ex] 5 + 4(2) \\[3ex] 5 + 4(\color{darkblue}{3} - 1) $ | 3 | 1, 2, 3 | $ \pi \cdot (\color{darkblue}{3})^2 \\[3ex] 9\pi $ | $ \pi \cdot (\color{darkblue}{3} - 1)^2 \\[3ex] \pi \cdot (2)^2 \\[3ex] 4\pi $ | $ 9\pi - 4\pi = 5\pi $ | $ 2\pi(1) + 2\pi(2) + 2\pi(3) \\[3ex] 2\pi + 4\pi + 6\pi \\[3ex] 12\pi \\[3ex] \implies \\[3ex] \pi \cdot 3 \cdot 4 \\[3ex] \pi \cdot \color{darkblue}{3} \cdot (\color{darkblue}{3} + 1) $ |
| 4 | $ 5 + 4 + 4 + 4 = 17 \\[3ex] \implies \\[3ex] 5 + 4(3) \\[3ex] 5 + 4(\color{darkblue}{4} - 1) $ | 4 | 1, 2, 3, 4 | $ \pi \cdot (\color{darkblue}{4})^2 \\[3ex] 16\pi $ | $ \pi \cdot (\color{darkblue}{4} - 1)^2 \\[3ex] \pi \cdot (3)^2 \\[3ex] 9\pi $ | $ 16\pi - 9\pi = 7\pi $ | $ 2\pi(1) + 2\pi(2) + 2\pi(3) + 2\pi(4) \\[3ex] 2\pi + 4\pi + 6\pi + 8\pi \\[3ex] 20\pi \\[3ex] \implies \\[3ex] \pi \cdot 4 \cdot 5 \\[3ex] \pi \cdot \color{darkblue}{4} \cdot (\color{darkblue}{4} + 1) $ |
| 5 | $ 5 + 4 + 4 + 4 + 4 = 21 \\[3ex] \implies \\[3ex] 5 + 4(4) \\[3ex] 5 + 4(\color{darkblue}{5} - 1) $ | 4 | 1, 2, 3, 4, 5 | $ \pi \cdot (\color{darkblue}{5})^2 \\[3ex] 25\pi $ | $ \pi \cdot (\color{darkblue}{5} - 1)^2 \\[3ex] \pi \cdot (4)^2 \\[3ex] 16\pi $ | $ 25\pi - 16\pi = 9\pi $ | $ 2\pi(1) + 2\pi(2) + 2\pi(3) + 2\pi(4) + 2\pi(5) \\[3ex] 2\pi + 4\pi + 6\pi + 8\pi + 10\pi \\[3ex] 30\pi \implies \\[3ex] \pi \cdot 5 \cdot 6 \\[3ex] \pi \cdot \color{darkblue}{5} \cdot (\color{darkblue}{5} + 1) $ |
| n | $ 5 + 4(\color{darkblue}{n} - 1) \\[3ex] 5 + 4n - 4 \\[3ex] 4n + 1 $ | n | $1, 2, 3, 4, 5, ..., n - 1, n$ | $ \pi \cdot (\color{darkblue}{n})^2 \\[3ex] \pi n^2 $ | $ \pi(\color{darkblue}{n} - 1)^2 $ | $ \pi n^2 - \pi(n - 1)^2 \\[3ex] \pi[n^2 - (n - 1)^2] \\[3ex] \pi[n^2 - (n - 1)(n - 1)] \\[3ex] \pi[n^2 - (n^2 - n - n + 1)] \\[3ex] \pi[n^2 - (n^2 - 2n + 1)] \\[3ex] \pi(n^2 - n^2 + 2n - 1) \\[3ex] \pi(2n - 1) $ | $ \implies \\[3ex] \pi \cdot n \cdot n + 1 \\[3ex] \pi \cdot \color{darkblue}{n} \cdot (\color{darkblue}{n} + 1) \\[3ex] \pi n(n + 1) $ |
$ (b.) \\[3ex] \underline{Figure\;n} \\[3ex] Number\;\;of\;\;dots = 541 \\[3ex] Number\;\;of\;\;dots = 4n + 1 \\[3ex] \implies \\[3ex] 4n + 1 = 541 \\[3ex] 4n = 541 - 1 \\[3ex] 4n = 540 \\[3ex] n = \dfrac{540}{4} \\[5ex] n = 135 \\[5ex] (c.) \\[3ex] \underline{Figure\;n} \\[3ex] Area\;\;of\;\;the\;\;LARGEST\;\;circle = \pi n^2 \\[3ex] \implies \\[3ex] \underline{Figure\;3p} \\[3ex] Area\;\;of\;\;the\;\;LARGEST\;\;circle = \pi (3p)^2 \\[4ex] = 9\pi p^2 $


