Vectors and Scalars

Welcome to Our Site

Good afternoon.
I greet you this day, Fri Apr 04 2025 15:02:43 GMT+0000 (Coordinated Universal Time).

These are the solutions to the CSEC past questions on the topics: Vectors and Scalars.
When applicable, the TI-84 Plus CE calculator (also applicable to TI-84 Plus calculator) solutions are provided for some questions.
The link to the video solutions will be provided for you. Please subscribe to the YouTube channel to be notified of upcoming livestreams. You are welcome to ask questions during the video livestreams.
If you find these resources valuable and helpful in your passing the Mathematics test of the CSEC, please consider making a donation:

Cash App: $ExamsSuccess or
cash.app/ExamsSuccess

PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess

Google charges me for the hosting of this website and my other educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well. As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.

Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.

Symbols and Formulas

(1.) A(x, y)
Point: A
(): parenthesis
x = x-coordinate
y = y-coordinate

(2.) A $\langle x, y \rangle$
Vector: A
$\langle \rangle$ : angle brackets
x = horizontal component
y = vertical component

(3.) Given a vector: $\overrightarrow{AB}$

$\overrightarrow{AB} = \vec{B} - \vec{A} \\[3ex] first\;\;vector = \vec{A} = \langle A_x, A_y \rangle \\[3ex] second\;\;vector = \vec{B} = \langle B_x, B_y \rangle \\[3ex] \overrightarrow{AB} = \langle B_x - A_x, B_y - A_y \rangle \\[3ex] \overrightarrow{AB} = -\overrightarrow{BA} \\[5ex]$ (4.) Given a vector: $\overrightarrow{BA}$

$\overrightarrow{BA} = \vec{A} - \vec{B} \\[3ex] first\;\;vector = \vec{B} = \langle B_x, B_y \rangle \\[3ex] second\;\;vector = \vec{A} = \langle A_x, A_y \rangle \\[3ex] \overrightarrow{BA} = \langle A_x - B_x, A_y - B_y \rangle \\[3ex] \overrightarrow{BA} = -\overrightarrow{AB} \\[5ex]$ (5.) Given several vectors:
Notice the colors and the pattern

$(a.)\;\; \overrightarrow{AB} = -\overrightarrow{BA} \\[3ex] (b.)\;\; \overrightarrow{CD} = -\overrightarrow{DC} \\[3ex] (c.)\;\; \overrightarrow{A\color{red}{K}} + \overrightarrow{\color{red}{K}C} = \overrightarrow{AC} \\[3ex] (d.)\;\; \overrightarrow{U\color{red}{K}} + \overrightarrow{\color{red}{K}S} = \overrightarrow{US} \\[3ex] (e.)\;\; \overrightarrow{M\color{red}{P}} + \overrightarrow{\color{red}{P}C} + \overrightarrow{\color{red}{C}D} = \overrightarrow{MD} \\[5ex]$ (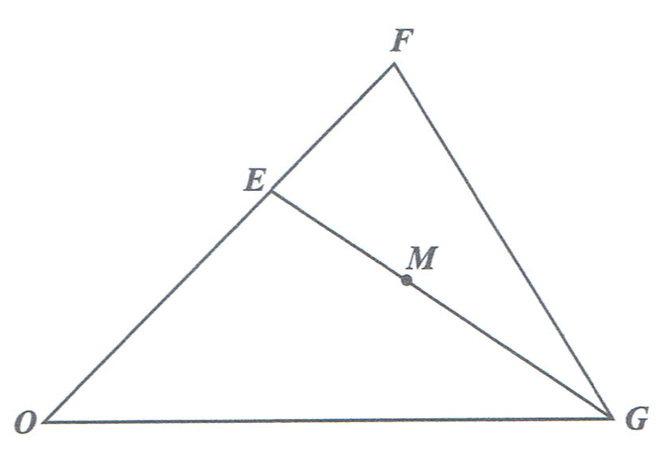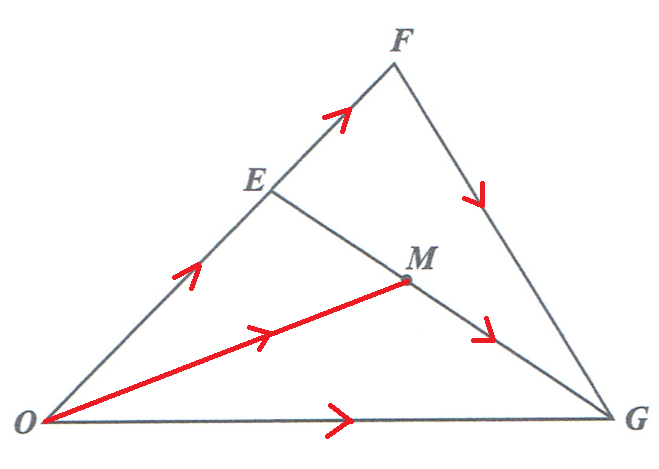6.) Given two position vectors: $\overrightarrow{OE}$ and $\overrightarrow{OF}$

$\overrightarrow{EF} = \overrightarrow{EO} + \overrightarrow{OF} \\[3ex] \overrightarrow{EF} = -\overrightarrow{OE} + \overrightarrow{OF} \\[5ex]$ (7.) Given vectors in component form OR unit vectors:
Say for a two-dimensional vector A:

$\boldsymbol{A}\langle x, y \rangle = x\boldsymbol{i} + y\boldsymbol{j} \\[3ex]$ Say for a three-dimensional vector C:

$\boldsymbol{C}\langle x, y, z \rangle = x\boldsymbol{i} + y\boldsymbol{j} + z\boldsymbol{k} \\[3ex]$ Sum and Difference of Vectors
Assume we have two two-dimensional vectors: C and D:

$\boldsymbol{C}\langle c_1, c_2 \rangle = c_1\boldsymbol{i} + c_2\boldsymbol{j} \\[3ex] \boldsymbol{D}\langle d_1, d_2 \rangle = d_1\boldsymbol{i} + d_2\boldsymbol{j} \\[5ex] \underline{Sum} \\[3ex] \vec{C} + \vec{D} \\[3ex] = \langle c_1 + d_1, c_2 + d_2 \rangle \\[3ex] = (c_1 + d_1)\boldsymbol{i} + (c_2 + d_2)\boldsymbol{j} \\[5ex] \underline{Difference} \\[3ex] \vec{C} - \vec{D} \\[3ex] = \langle c_1 - d_1, c_2 - d_2 \rangle \\[3ex] = (c_1 - d_1)\boldsymbol{i} + (c_2 - d_2)\boldsymbol{j} \\[5ex]$ Assume we have two three-dimensional vectors: C and D:

$\boldsymbol{C}\langle c_1, c_2, c_3 \rangle = c_1\boldsymbol{i} + c_2\boldsymbol{j} + c_3\boldsymbol{k} \\[3ex] \boldsymbol{D}\langle d_1, d_2, d_3 \rangle = d_1\boldsymbol{i} + d_2\boldsymbol{j} + d_3\boldsymbol{j} \\[5ex] \underline{Sum} \\[3ex] \vec{C} + \vec{D} \\[3ex] = \langle c_1 + d_1, c_2 + d_2, c_3 + d_3 \rangle \\[3ex] = (c_1 + d_1)\boldsymbol{i} + (c_2 + d_2)\boldsymbol{j} + (c_3 + d_3)\boldsymbol{k} \\[5ex] \underline{Difference} \\[3ex] \vec{C} - \vec{D} \\[3ex] = \langle c_1 - d_1, c_2 - d_2, c_3 - d_3 \rangle \\[3ex] = (c_1 - d_1)\boldsymbol{i} + (c_2 - d_2)\boldsymbol{j} + (c_3 - d_3)\boldsymbol{k} \\[5ex]$ (8.) A displacement vector say $\overrightarrow{OA}$ beginning from the origin, O and ending at the point A is the position vector, $\overrightarrow{A}$

(9.) Section Formula
Given two points say A and B with position vectors: $\overrightarrow{A}$ and $\overrightarrow{B}$ respectively, if a point say C divides the line segment |AC| in the ratio: m:n, then the position vector of C is given by: $\overrightarrow{C} = \dfrac{m\overrightarrow{B} + n\overrightarrow{A}}{m + n} \\[5ex]$ (10.) Collinearity of Points using Vectors
Given two vectors say: $\overrightarrow{A}$ and $\overrightarrow{B}$ and a scalar say k:

$Say: \overrightarrow{A} = \langle a_1, a_2 \rangle \\[5ex] \overrightarrow{B} = \langle b_1, b_2 \rangle \\[5ex]$ (a.) Scalar Multiple Method
The two vectors are collinear if one is a scalar multiple of the other.
(This concept also demonstrates the linear dependency of two vectors.)
OR
The two vectors are collinear if the ratio of their corresponding components are equal.

$\overrightarrow{A} = k \cdot \overrightarrow{B} \\[5ex] OR \\[3ex] \dfrac{a_1}{b_1} = \dfrac{a_2}{b_2} \\[6ex]$ (b.) Method of Determinants
Two vectors are collinear if their determinant is zero.

$\begin{vmatrix} a_1 & a_2 \\[4ex] b_1 & b_2 \end{vmatrix} = a_1b_2 - b_1a_2 = 0 \\[7ex]$ (c.) Dot Product Angle Between the Vectors
If the dot product angle between the two vectors is 0° or 180°, then the two vectors are collinear.

$\overrightarrow{A} \cdot \overrightarrow{B} = |\overrightarrow{A}| |\overrightarrow{B}| \cos \theta \\[3ex] where \\[3ex] \theta = \text{dot product angle between the two vectors} \\[5ex]$ (11.) Parallelism of Vectors
Given two vectors, say $\overrightarrow{A}$ and $\overrightarrow{B}$ :
Assume a scalar, say k
We can determine if the two vectors are parallel using any of these approaches.

(a.) Direction Vectors
Direction vectors indicate the orientation of a line.
Parallel lines have proportional direction vectors.
Two vectors are parallel if they lie on lines with equations that differ only by a scalar multiple.

(b.) Dot Product
Given the direction of the vectors, the dot product is: $A \cdot B = |A| \cdot |B| \cdot \cos\theta \\[3ex]$ where θ is the angle between the vectors.
If θ = 0° or θ = 180°, the vectors are parallel.

(c.) Scalar Multiples
Vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ are parallel if $\overrightarrow{B} = k \cdot \overrightarrow{A}$
Also:
If $A = (a_1, a_2, a_3, ...)$ and $B = (b_1, b_2, b_3, ...)$ :
the vectors are parallel if the ratio of the corresponding components are equal

$\dfrac{b_1}{a_1} = \dfrac{b_2}{a_2} = \dfrac{b_3}{a_3} = k \\[5ex]$ If both vectors are zero vectors, they are considered parallel.
If one vector is a zero vector and the other is not, they are not parallel.
If any calculation of ratios result in undefined values (e.g., dividing by zero), the vectors are not parallel.

(d.) Cross Product (for 3D vectors)
Two vectors are parallel if the cross product: $A \times B$ is zero.
The cross product measures the area of the parallelogram spanned by the two vectors.
An area of zero units means that the vectors lie along the same or parallel lines.

Formula Sheet: List of Formulae

Theorems

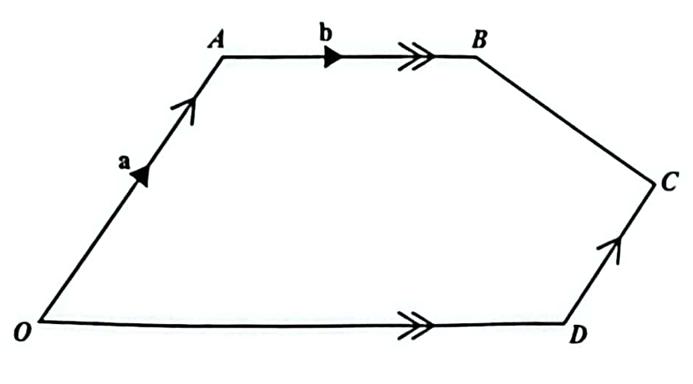
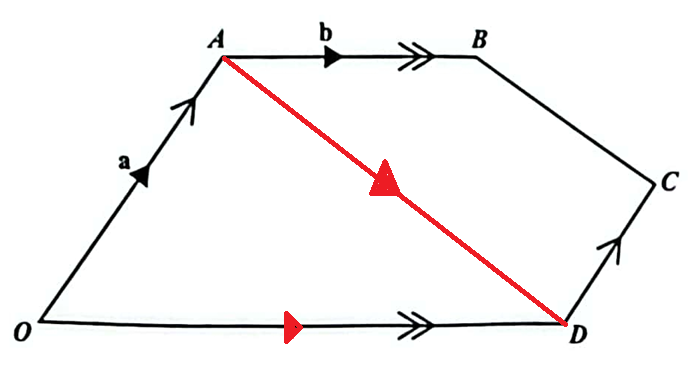
(1.) Proportional Segments Theorem for Diagonals in a Quadrilateral
In a quadrilateral, the line segment joining two points that divide opposite sides proportionally or at specific ratios from a common vertex is parallel to and proportional to the diagonal that does not connect to the vertex.

(1.) In the diagram below, O is the origin, OE = 2EF and M is the midpoint of EG.

$\overrightarrow{OG} = c$ and

$\overrightarrow{OF} = d$

Number 1

Find in terms of c and d, in its simplest form,
(i.)

$\overrightarrow{FG}$
(ii.)

$\overrightarrow{EG}$
(iii.)

$\overrightarrow{OM}$

Let us update the diagram

Number 1

$\overrightarrow{OF} = \overrightarrow{F} = d...\text{from the origin} \\[3ex] \overrightarrow{OG} = \overrightarrow{G} = c ...\text{from the origin} \\[3ex] \overrightarrow{MG} = \dfrac{1}{2}\overrightarrow{EG}...\text{M is the midpoint of } \overrightarrow{EG} \\[3ex] \overrightarrow{OE} = \overrightarrow{E} ...\text{from the origin} \\[3ex] \overrightarrow{OE} = 2\overrightarrow{EF} \\[3ex] \overrightarrow{OF} = \overrightarrow{OE} + \overrightarrow{EF} ...diagram \\[3ex] = 2\overrightarrow{EF} + \overrightarrow{EF} \\[3ex] = 3\overrightarrow{EF} \\[3ex] \implies \\[3ex] d = 3\overrightarrow{EF} \\[3ex] \overrightarrow{EF} = \dfrac{d}{3} \\[5ex] So,\;\;\overrightarrow{OE} = \overrightarrow{E} = 2\left(\dfrac{d}{3}\right) = \dfrac{2d}{3} \\[5ex]$ We can solve (i.) and (ii.) using at least two approaches.
Use any approach you prefer.

$(i.) \\[3ex] \underline{\text{1st Approach: Formula Definition}} \\[3ex] \overrightarrow{FG} = \overrightarrow{G} - \overrightarrow{F} \\[3ex] = c - d \\[5ex] \underline{\text{2nd Approach}} \\[3ex] \underline{\triangle EFG} \\[3ex] \overrightarrow{EG} = \overrightarrow{EF} + \overrightarrow{FG}...eqn.(1.) \\[5ex] \underline{\triangle OEG} \\[3ex] \overrightarrow{OG} = \overrightarrow{OE} + \overrightarrow{EG} \\[3ex] \overrightarrow{EG} = \overrightarrow{OG} - \overrightarrow{OE}...eqn.(2.) \\[5ex] \overrightarrow{EG} = \overrightarrow{EG} \implies eqn.(1) = eqn.(2) \\[3ex] \overrightarrow{EF} + \overrightarrow{FG} = \overrightarrow{OG} - \overrightarrow{OE} \\[3ex] \overrightarrow{FG} = \overrightarrow{OG} - \overrightarrow{OE} - \overrightarrow{EF} \\[3ex] = c - \dfrac{2d}{3} - \dfrac{d}{3} \\[5ex] = c - \dfrac{3d}{3} \\[5ex] = c - d \\[5ex] (ii.) \\[3ex] \underline{\text{1st Approach: Formula Definition}} \\[3ex] \overrightarrow{EG} = \overrightarrow{G} - \overrightarrow{E} \\[3ex] = c - \dfrac{2d}{3} \\[5ex] = \dfrac{c}{1} - \dfrac{2d}{3} \\[5ex] = \dfrac{3c - 2d}{3} \\[5ex] \underline{\text{2nd Approach}} \\[3ex] \text{Use any of the equations.} \\[3ex] \text{It should give the same answer.} \\[3ex] \text{From eqn.(2)} \\[3ex] \overrightarrow{EG} = \overrightarrow{OG} - \overrightarrow{OE} \\[3ex] = c - \dfrac{2d}{3} \\[5ex] = \dfrac{3c - 2d}{3} \\[5ex] OR \\[3ex] \text{From eqn.(1)} \\[3ex] \overrightarrow{EG} = \overrightarrow{EF} + \overrightarrow{FG} \\[3ex] = \dfrac{d}{3} + (c - d) \\[5ex] = \dfrac{d}{3} + \dfrac{c - d}{1} \\[5ex] = \dfrac{d + 3(c - d)}{3} \\[5ex] = \dfrac{d + 3c - 3d}{3} \\[5ex] = \dfrac{3c - 2d}{3} \\[5ex] (iii.) \\[3ex] \underline{\triangle OMG} \\[3ex] \overrightarrow{OG} = \overrightarrow{OM} + \overrightarrow{MG} \\[3ex] \overrightarrow{OM} = \overrightarrow{OG} - \overrightarrow{MG} \\[3ex] = c - \dfrac{3c - 2d}{6} \\[5ex] = \dfrac{c}{1} - \dfrac{3c - 2d}{6} \\[5ex] = \dfrac{6c -(3c - 2d)}{6} \\[5ex] = \dfrac{6c - 3c + 2d}{6} \\[5ex] = \dfrac{3c + 2d}{6}$

(2.)

$\overrightarrow{PQ} = \begin{bmatrix} 5 \\[2ex] -4 \end{bmatrix} \\[5ex]$ If P is the point (−2, 3), determine the coordinates of Q.

$\overrightarrow{PQ} = \overrightarrow{Q} - \overrightarrow{P} \\[4ex] \overrightarrow{Q} = \overrightarrow{PQ} + \overrightarrow{P} \\[4ex] = \begin{bmatrix} 5 \\[2ex] -4 \end{bmatrix} + (-2, 3) \\[5ex] = (5, -4) + (-2, 3) \\[3ex] = (5 + -2, -4 + 3) \\[3ex] = (3, -1)$

(7.) In the pentagon OABCD, OA is parallel to DC and AB is parallel to OD.
OD = 2AB and OA = 2DC.

$\overrightarrow{OA} = a$ and

$\overrightarrow{AB} = b$

Number 7

Find, in terms of a and b, in its simplest form,
(i.)

$\overrightarrow{AD}$
(ii.)

$\overrightarrow{BC}$
(iii.) State the conclusion about

$|\overrightarrow{AD}|$ and

$|\overrightarrow{BC}|$ that can be drawn from your responses in (i.) and (ii.)

$\overrightarrow{OA} = a \\[3ex] \overrightarrow{AB} = b \\[3ex] OD = 2AB \\[3ex] OA = 2DC \\[3ex] 2DC = OA \\[3ex] DC = \dfrac{OA}{2} = \dfrac{a}{2} \\[5ex]$ (i.) Let us indicate it on the diagram
Number 7-1st

$\overrightarrow{OD} = \overrightarrow{OA} + \overrightarrow{AD} \\[4ex] \overrightarrow{AD} = \overrightarrow{OD} - \overrightarrow{OA} \\[4ex] = 2AB - 2DC \\[3ex] = 2b - 2\left(\dfrac{a}{2}\right) \\[5ex] = 2b - a \\[3ex]$ (ii.) Let us indicate it on the diagram
Number 7-2nd

$\overrightarrow{BD} = \overrightarrow{BC} + \overrightarrow{CD} \\[3ex] \overrightarrow{BC} = \overrightarrow{BD} - \overrightarrow{CD} \\[3ex] = \overrightarrow{BD} - (-\overrightarrow{DC}) \\[3ex] = \overrightarrow{BD} + \overrightarrow{DC} \\[3ex] = (b - a) + \dfrac{a}{2} \\[5ex] = b - a + \dfrac{a}{2} \\[5ex] = b - \dfrac{a}{2} \\[5ex] (iii) \\[3ex] \overrightarrow{BC} = b - \dfrac{a}{2} \\[5ex] \overrightarrow{AD} = 2b - a \\[5ex] \text{Any relationship}? \\[3ex] 2 \cdot \overrightarrow{BC} \\[3ex] = 2\left(b - \dfrac{a}{2}\right) \\[5ex] = 2b - a \\[3ex] = \overrightarrow{AD} \\[3ex] \therefore \overrightarrow{AD} = 2\overrightarrow{BC} \\[3ex]$ This implies that

$\overrightarrow{AD}$ and

$\overrightarrow{BC}$ are parallel vectors because one is a scalar multiple of the other.

(9.) The diagram below shows quadrilateral OLMN, in which O is the origin,

$\overrightarrow{OL} = 4y$ ,

$\overrightarrow{OM} = 6z$ and

$\overrightarrow{ON} = 2x$
The point A lies on LM such that LA : AM = 1 : 2 and the point B on MN such MB : BN = 2 : 1.

Number 9

(a.) Express, in its simplest form,

$\overrightarrow{MN}$ in terms of x and z

(b.) Find, in terms of x and y, in its simplest form, an expression for

$\overrightarrow{LN}$

(c.) Show that

$\overrightarrow{AB}$ equals

$\dfrac{2}{3}(2x - 4y)$

(d.) Based on your results in Parts (b.) and (c.), state TWO properties relating LN to AB.

$(a.) \\[3ex] \overrightarrow{OM} + \overrightarrow{MN} = \overrightarrow{ON} \\[3ex] \overrightarrow{MN} = \overrightarrow{ON} - \overrightarrow{OM} \\[3ex] = 2x - 6z \\[3ex] = 2(x - 3z) \\[3ex]$ (b.) Let us join Point L to Point N

Number 9-1st

$\overrightarrow{OL} + \overrightarrow{LN} = \overrightarrow{ON} \\[3ex] \overrightarrow{LN} = \overrightarrow{ON} - \overrightarrow{OL} \\[3ex] = 2x - 4y \\[3ex] = 2(x - 2y) \\[3ex]$ (c.) Let us join Point A to Point B

Number 9-2nd

There are at least two approaches that we can use to solve this question.
Use any approach that you prefer.

1st Approach: Proportional Segments Theorem for Diagonals in a Quadrilateral

$|AB| \;\;||\;\; |LN| ...\text{Proportional Segments Theorem for Diagonal} \\[3ex] \implies \\[3ex] \underline{\triangle AMB \;\;and\;\; \triangle LMN} \\[3ex] \angle MAB = \angle MLN ...\text{corresponding angles are congruent} \\[3ex] \angle MBA = \angle MNL ...\text{corresponding angles are congruent} \\[3ex] \implies \\[3ex] \triangle AMB \sim \triangle LMN ...\text{Angle – Angle Similarity Postulate} \\[3ex] \implies \\[3ex] \dfrac{\overrightarrow{AB}}{\overrightarrow{LN}} = \dfrac{\overrightarrow{MB}}{\overrightarrow{MN}}...\text{ratio of corresponding sides} \\[6ex] MB : BN = 2 : 1 ...Given \\[3ex] \dfrac{MB}{BN} = \dfrac{2}{1} \\[5ex] MB = 2\cdot BN = 2BN \\[3ex] Also: \\[3ex] MN = MB + BN ...diagram \\[3ex] MN = 2BN + BN \\[3ex] MN = 3BN \\[3ex] \text{Substitute MN = 3BN and the values for LN and MB} \\[3ex] \implies \\[3ex] \dfrac{\overrightarrow{AB}}{\overrightarrow{LN}} = \dfrac{\overrightarrow{MB}}{\overrightarrow{MN}} \\[5ex] \dfrac{\overrightarrow{AB}}{2x - 4y} = \dfrac{2\overrightarrow{BN}}{3\overrightarrow{BN}} \\[6ex] \overrightarrow{AB} = \dfrac{2}{3}(2x - 4y) \\[5ex]$ 2nd Approach: Formulas

$\underline{\text{Position Vectors}} \\[3ex] \overrightarrow{OL} = \overrightarrow{L} = 4y \\[4ex] \overrightarrow{OM} = \overrightarrow{M} = 6z \\[4ex] \overrightarrow{ON} = \overrightarrow{N} = 2x \\[5ex] \underline{\text{Section Formulas}} \\[3ex] \text{Point A divides |LM| in the ratio of 1 : 2} \\[3ex] \overrightarrow{A} = \dfrac{1 \cdot \overrightarrow{M} + 2 \cdot \overrightarrow{L}}{1 + 2} \\[6ex] = \dfrac{\overrightarrow{M} + 2\overrightarrow{L}}{3} \\[6ex] = \dfrac{6z + 2(4y)}{3} \\[5ex] = \dfrac{6z + 8y}{3} \\[7ex] \text{Point B divides |MN| in the ratio of 2 : 1} \\[3ex] \overrightarrow{B} = \dfrac{2 \cdot \overrightarrow{N} + 1 \cdot \overrightarrow{M}}{2 + 1} \\[6ex] = \dfrac{2\overrightarrow{N} + \overrightarrow{M}}{3} \\[6ex] = \dfrac{2(2x) + 1(6z)}{3} \\[5ex] = \dfrac{4x + 6z}{3} \\[7ex] \text{Let us find } \overrightarrow{AB} \\[4ex] \overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} ...Definition \\[4ex] = \dfrac{4x + 6z}{3} - \dfrac{6z + 8y}{3} \\[5ex] = \dfrac{(4x + 6z) - (6z + 8y)}{3} \\[5ex] = \dfrac{4x + 6z - 6z - 8y}{3} \\[5ex] = \dfrac{4x - 8y}{3} \\[5ex] = \dfrac{2(2x - 4y)}{3} \\[5ex] = \dfrac{2}{3}\overrightarrow{LN} \\[5ex]$ (c.) The geometric properties relating LN to AB are:

(i.) Proportional Segments Theorem for Diagonal: This indicates that |AB| is parallel to |LN|

(ii.) Linear Dependence: This is because

$\overrightarrow{AB}$ is a scalar multiple of

$\overrightarrow{LN}$ :

$\overrightarrow{AB} = \dfrac{2}{3}\overrightarrow{LN} \\[5ex]$ Hence

$\overrightarrow{AB}$ and

$\overrightarrow{LN}$ are linearly dependent vectors.

Top