Geometry
Welcome to Our Site
I greet you this day,
These are the solutions to the GCSE past questions on the topics in Geometry.
When applicable, the TI-84 Plus CE calculator (also applicable to TI-84 Plus calculator) solutions are provided
for some questions.
The link to the video solutions will be provided for you. Please
subscribe to the YouTube channel to be notified of upcoming livestreams. You are welcome to ask questions during
the video livestreams.
If you find these resources valuable and if any of these resources were helpful in your passing the
Mathematics test of the GCSE, please consider making a donation:
Cash App: $ExamsSuccess or
cash.app/ExamsSuccess
PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess
Google charges me for the hosting of this website and my other
educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well.
As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.
Comments, ideas, areas of improvement, questions, and constructive
criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.
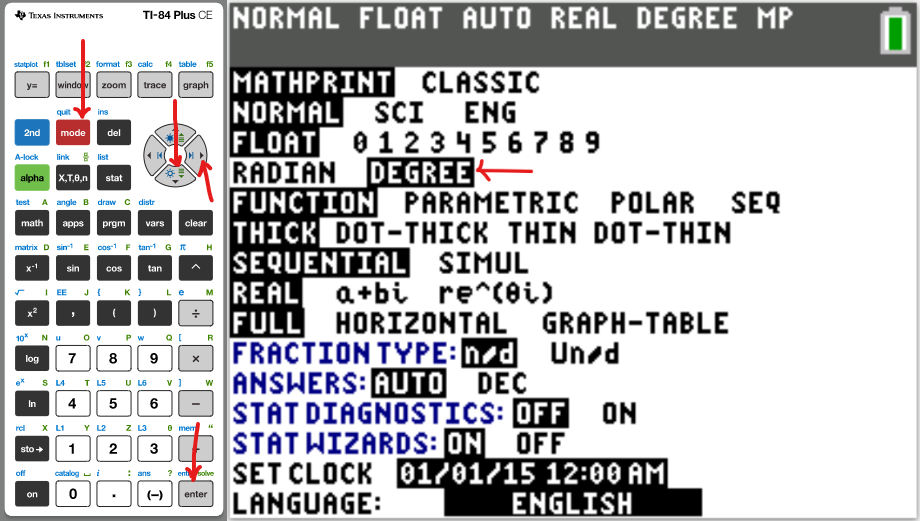
Please NOTE: For applicable questions (questions that require the angle in degrees), if you intend to
use the TI-84 Family:
Please make sure you set the MODE to DEGREE.
It is RADIAN by default. So, it needs to be set to DEGREE.
Formulas
(1.) $\overleftrightarrow{AB}$Line AB
(2.) $\overline{AB}$
Line Segment AB
(3.) $\overrightarrow{AB}$
Ray AB
(4.) Given: n collinear points:
the number of different rays that can be named is: 2(n − 1) rays.
(5.) Given: n collinear points:
the number of different lines that can be named if order is important is found from the Permutation formula.
Two points are used to name a line.
Permutation: order is important: perm 2 from n
$P(n, 2) = \dfrac{n!}{(n - 2)!}$
(6.) Given: n collinear points:
the number of different lines that can be named if order is not important is found from the Combination formula.
Two points are used to name a line.
Combination: order is not important: comb 2 from n
$C(n, 2) = \dfrac{n!}{(n - 2)! * 2!}$
(7.) Given: n coplanar points:
the number of different ways to name the plane if order is important is found from the Permutation formula.
Three points are used to name a plane.
Permutation: order is important: perm 3 from n
$P(n, 3) = \dfrac{n!}{(n - 3)!}$
(8.) Given: n coplanar points:
the number of different ways to name the plane if order is not important is found from the Combination formula.
Three points are used to name a plane.
Combination: order is not important: comb 3 from n
$C(n, 3) = \dfrac{n!}{(n - 3)! * 3!}$
(9.) Regular Polygons
Where: the number of sides is greater than 4
Let:
number of sides = n
side length = s
radius (the distance from the center to a vertex) = r
apothem (shortest distance from the center to one of the sides) = a
each interior angle = θ
perimeter = P
area = A
$ \Sigma \theta = 180^\circ(n - 2) \\[3ex] \theta = \dfrac{180^\circ(n - 2)}{n} \\[5ex] a = r\cos\left(\dfrac{180^\circ}{n}\right) \\[6ex] a = \dfrac{s}{2\tan \left(\dfrac{180^\circ}{n}\right)} \\[8ex] s = 2r\sin\left(\dfrac{180^\circ}{n}\right) \\[6ex] s = 2a\tan\left(\dfrac{180^\circ}{n}\right) \\[7ex] r = \dfrac{a}{\cos\left(\dfrac{180^\circ}{n}\right)} \\[8ex] r = \dfrac{s}{2\sin\left(\dfrac{180^\circ}{n}\right)} \\[8ex] P = ns \\[3ex] P = 2rn\sin\left(\dfrac{180^\circ}{n}\right) \\[6ex] P = 2an\tan\left(\dfrac{180^\circ}{n}\right) \\[6ex] A = \dfrac{\pi r^2}{2}\sin\left(\dfrac{360^\circ}{n}\right) \\[7ex] A = \dfrac{aP}{2} \\[5ex] A = \dfrac{ans}{2} \\[5ex] A = \dfrac{\pi a^2}{\cos^2\left(\dfrac{180^\circ}{n}\right)} \sin\left(\dfrac{360^\circ}{n}\right) \\[7ex] \text{Sum of interior angles} = 180(n - 2) \\[4ex] \text{Each interior angle} = \dfrac{180(n - 2)}{n} \\[6ex] \text{Sum of exterior angles} = 360^\circ \\[4ex] \text{Each interior angle} = \dfrac{360}{n} \\[6ex] $ (10.) Section Formula
Given two points say A(x1, y1) and B(x2, y2): if a point say C(x, y) divides the line segment |AB| in the ratio: m:n, then the coordinates of C is given by:
$ C = \dfrac{mB + nA}{m + n} \\[5ex] C(x, y) = \left(\dfrac{mx_2 + nx_1}{m + n}, \dfrac{my_2 + ny_1}{m + n}\right) $
- Symbols and Meanings for Circles
- (h, k) = coordinates of the center of a circle
- r = radius of a circle
- d = diameter of a circle
- C = circumference of a circle (also known as the perimeter)
- A = area of a circle
- π = pi = $\dfrac{22}{7}$
- θ = central angle
- ° = DEG = degrees
- RAD = radians
- L = length of arc
- Asec = area of sector
- Psec = perimeter of sector
- Aseg = area of segment
- Pseg = perimeter of segment
- (x1, y1) = first endpoint of the diameter of a circle
- (x2, y2) = second endpoint of the diameter of a circle
Radius, Diameter, Circumference, Area
$ \underline{Circle} \\[3ex] d = 2r \\[3ex] r = \dfrac{d}{2} \\[5ex] C = \pi d \\[3ex] d = \dfrac{C}{\pi} \\[5ex] C = 2\pi r \\[3ex] r = \dfrac{C}{2\pi} \\[5ex] A = \pi r^2 \\[3ex] r = \sqrt{\dfrac{A}{\pi}} \\[5ex] A = \dfrac{\pi d^2}{4} \\[5ex] d = \sqrt{\dfrac{4A}{\pi}} \\[5ex] A = \dfrac{C^2}{4\pi} \\[5ex] C = 2\sqrt{A\pi} \\[5ex] \underline{Semicircle} \\[3ex] d = 2r \\[3ex] r = \dfrac{d}{2} \\[5ex] C = \pi r \\[3ex] C = \dfrac{\pi d}{2} \\[5ex] r = \dfrac{C}{\pi} \\[5ex] d = \dfrac{2C}{\pi} \\[5ex] A = \dfrac{\pi r^2}{2} \\[5ex] r = \sqrt{\dfrac{2A}{\pi}} \\[5ex] A = \dfrac{\pi d^2}{8} \\[5ex] d = \sqrt{\dfrac{8A}{\pi}} \\[7ex] \underline{\theta\;\;in\;\;DEG} \\[3ex] L = \dfrac{2\pi r\theta}{360} \\[5ex] \theta = \dfrac{180L}{\pi r} \\[5ex] r = \dfrac{180L}{\pi \theta} \\[5ex] A_{sec} = \dfrac{\pi r^2\theta}{360} \\[5ex] P_{sec} = \dfrac{r(\pi\theta + 360)}{180} \\[5ex] \theta = \dfrac{360A_{sec}}{\pi r^2} \\[5ex] r = \dfrac{360A_{sec}}{\pi\theta} \\[5ex] A_{sec} = \dfrac{Lr}{2} \\[5ex] A_{sec} = \dfrac{Lr}{2} \\[5ex] r = \dfrac{2A_{sec}}{L} \\[5ex] L = \dfrac{2A_{sec}}{r} \\[5ex] \underline{\theta\;\;in\;\;RAD} \\[3ex] L = r\theta \\[5ex] \theta = \dfrac{L}{r} \\[5ex] r = \dfrac{L}{\theta} \\[5ex] A_{sec} = \dfrac{r^2\theta}{2} \\[5ex] \theta = \dfrac{2A_{sec}}{r^2} \\[5ex] r = \sqrt{\dfrac{2A_{sec}}{\theta}} \\[5ex] $ (1.) Standard Form of the Equation of a Circle
$(x - h)^2 + (y - k)^2 = r^2$
where:
$x, y$ are the variables
$(h, k)$ are the coordinates of the center of the circle
$r$ is the radius of the circle
(2.) General Form of the Equation of a Circle
$x^2 + y^2 + 2gx + 2fy + c = 0$
where:
$x, y$ are the variables
$c$ is the coefficient of $x$
$d$ is the coefficient of $y$
$c, d, e$ are values/constants
(3.) Given: The Center Coordinates of a Circle and an Endpoint on the Circumference of the Circle
The coordinates of the center of the circle = $(h, k)$
The endpoint on the circumference of the circle = $(x_1, y_1)$
The radius of the circle can be found by the Distance Formula
The radius of the circle = $r$
r = $\sqrt{(x_1 - h)^2 + (y_1 - k)^2}$
The diameter of the circle = $d$
The diameter of the circle is twice the radius.
$d = 2 * r$
The second endpoint of the diameter of the circle can also be found
The second endpoint of the diameter of the circle = $(x_2, y_2)$
$ x_2 = x_1 + r \\[3ex] y_2 = y_1 + r \\[3ex] (x_2, y_2) = (x_1 + r, y_1 + r) \\[3ex] $ (4.) Given: The Endpoints of the Diameter of the Circle
$(x_1, y_1)$ = first endpoint of the diameter of a circle
$(x_2, y_2)$ = second endpoint of the diameter of a circle
The center of the circle is found using the Midpoint Formula
$(h, k)$ are the coordinates of the center of the circle
$ h = \dfrac{x_1 + x_2}{2} \\[5ex] k = \dfrac{y_1 + y_2}{2} \\[5ex] $ Euler's Theorem: The number of faces (F ), vertices (V ), and edges (E ) of a polyhedron are related by the formula: F + V = E + 2
⇒ F + V − E = 2
In naming a line, two points are used.
In naming a plane, three points are used.
We can measure angles in:
Degrees (DEG, $^\circ$)
Radians (RAD)
Gradians (GRAD)
Degrees, Minutes, and Seconds ($^\circ \:'\:''$)
$DRG$ means $Degree-Radian-Gradian$ in some calculators
$180^\circ = \pi \:\:RAD = 200 \:\:GRAD$
To convert from:
radians to degrees, multiply by $\dfrac{180}{\pi}$
degrees to radians, multiply by $\dfrac{\pi}{180}$
$DMS$ means $Degree-Minute-Second$ in some calculators
$ 1^\circ = 60' \\[3ex] 1^\circ = 3600'' \\[3ex] 1^\circ = 60' = 3600'' \\[3ex] 1' = 60'' \\[3ex] $ To convert from:
degrees to minutes, multiply by $60$
minutes to degrees, divide by $60$
degrees to seconds, multiply by $3600$
seconds to degrees, divide by $3600$
minutes to seconds, multiply by $60$
seconds to minutes, divide by $60$
Show students these angular measures in their scientific calculators.
Show them how to convert from one angular measure to another.
Ellipses
- Symbols and Meanings for Ellipses
- (h, k) = coordinates of the center of an ellipse
- Ellipse: a = horizontal distance from the center to the boundary
- Ellipse: b = vertical distance from the center to the boundary
- Horizontal Ellipse: a = half the length of the major axis OR the length of the semi-major axis
- Horizontal Ellipse: b = half the length of the minor axis OR the length of the semi-minor axis
- Vertical Ellipse: a = half the length of the minor axis OR the length of the semi-minor axis
- Vertical Ellipse: b = half the length of the major axis OR the length of the semi-major axis
- c = linear eccentricity = distance from the center of the ellipse to the foci
- $f_1,f_2$ = foci points
- $f$ = distance between the foci
- e = eccentricity
- A = area
- P = perimeter
- L = length of the latus rectum
- $L_1,\;L_2,\;L_3,\;L_4$ = endpoints of the latus rectum
- D = distance between the two directrixes
- C = fractional factorials binomial coefficient
- λ = square of the ratio of the difference of the semi-axis to the sum of the semi-axis
- n = number of terms
(1.) Standard Form of the Equation of an Ellipse
$ \dfrac{(x - h)^2}{a^2} + \dfrac{(y - k)^2}{b^2} = 1 \\[5ex] $ If $a \gt b$, the ellipse is a horizontal ellipse.
If $a \lt b$, the ellipse is a vertical ellipse.
$ \underline{\text{Assume a Horizontal Ellipse}} \\[3ex] \text{Length of Major Axis} = 2a \\[3ex] \text{Length of Minor Axis} = 2b \\[3ex] \text{Distance between two Foci} = 2\sqrt{a^2 - b^2} \\[5ex] $ (2.) Eccentricity
$ e = \dfrac{\sqrt{semiMajor\;\;axis\;\;length^2 - semiMinor\;\;axis\;\;length^2}}{semiMajor\;\;axis\;\;length} \\[3ex] $ In other words:
Eccentricity: Horizontal Ellipse:
Major axis is the horizontal axis
Semi-major axis length = a
$ e = \dfrac{\sqrt{a^2 - b^2}}{a} \\[3ex] $ Eccentricity: Vertical Ellipse:
Major axis is the vertical axis
Semi-major axis length = b
$ e = \dfrac{\sqrt{b^2 - a^2}}{b} \\[5ex] $
Theorems
(1.) The sum of the interior angles of a triangle is 180°
(2.) The exterior angle of a triangle is the sum of the two interior opposite angles.
(3.) The sum of angles on a straight line is 180°
(4.) The sum of the angles at a point is 360°
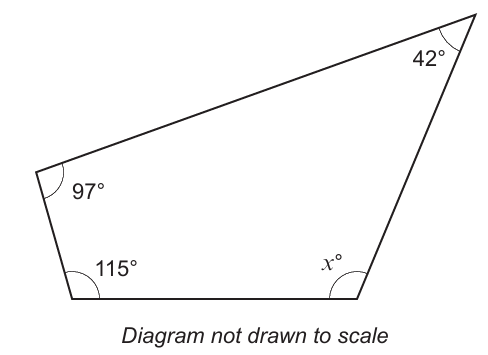
(5.) Interior Angle Sum Theorem: The sum of the interior angles of a polygon (regular and irregular
polygons) is $180(n - 2)$ where n is the number of sides.
This is because any polygon of n sides can be split into n − 2 triangles.
(6.) Exterior Angle Sum Theorem: The sum of the exterior angles of a polygon (regular and irregular
polygons) is 360°
(7.) Angle Bisector Theorem: Any point on the bisector of an angle is equidistant from the two sides of
the
angle.