☰ Please Read Me.

Non-Calculator Paper: Track 3: Year 11

Welcome to Our Site


I greet you this day,
These are the solutions to the Mathematics past questions for Non-Calculator Paper: Track 2: Year 11.
The link to the video solutions will be provided for you. Please subscribe to the YouTube channel to be notified of upcoming livestreams. You are welcome to ask questions during the video livestreams.
If you find these resources valuable and if any of these resources were helpful in your passing the Mathematics tests/exams, please consider making a donation:

Cash App: $ExamsSuccess or
cash.app/ExamsSuccess

PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess

Google charges me for the hosting of this website and my other educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well. As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.

Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.

(1.) Estimate the value of: $96 \div \sqrt{25.4}$


$ 25.4 \approx 25 \\[3ex] \sqrt{25} = 5 \\[3ex] 96 \div 5 \\[3ex] = 19 + \dfrac{1}{5} \\[5ex] = 19 + 0.2 \\[3ex] = 19.2 \\[3ex] \implies \\[3ex] 96 \div \sqrt{25.4} \approx 19.2 $
(2.) The area of France is about 552 thousand square kilometres.
Write this number in standard form.


$ 552000 \;km^2 \\[4ex] = 552 * 1000 \\[3ex] = 5.52 * 100 * 1000 \\[3ex] = 5.52 * 10^5\;km^2 $
(3.) Circle the value of the digit 6 in the number 12.368

$ \dfrac{6}{1000} \hspace{5em} 6 \hspace{5em} \dfrac{6}{100} \hspace{5em} \dfrac{6}{10} \\[5ex] $

$ 12.368 \\[3ex] 6 \rightarrow 6 \;hundredth \\[3ex] = \dfrac{6}{100} $
(4.) Solve: $\dfrac{x}{7} - 6 = 3$


$ \dfrac{x}{7} - 6 = 3 \\[5ex] \dfrac{x}{7} = 3 + 6 \\[5ex] \dfrac{x}{7} = 9 \\[5ex] x = 7(9) \\[3ex] x = 63 \\[3ex] $ Check
$x = 63$
LHS RHS
$ \dfrac{x}{7} - 6 \\[5ex] \dfrac{63}{7} - 6 \\[5ex] 9 - 6 \\[3ex] 3 $ $3$
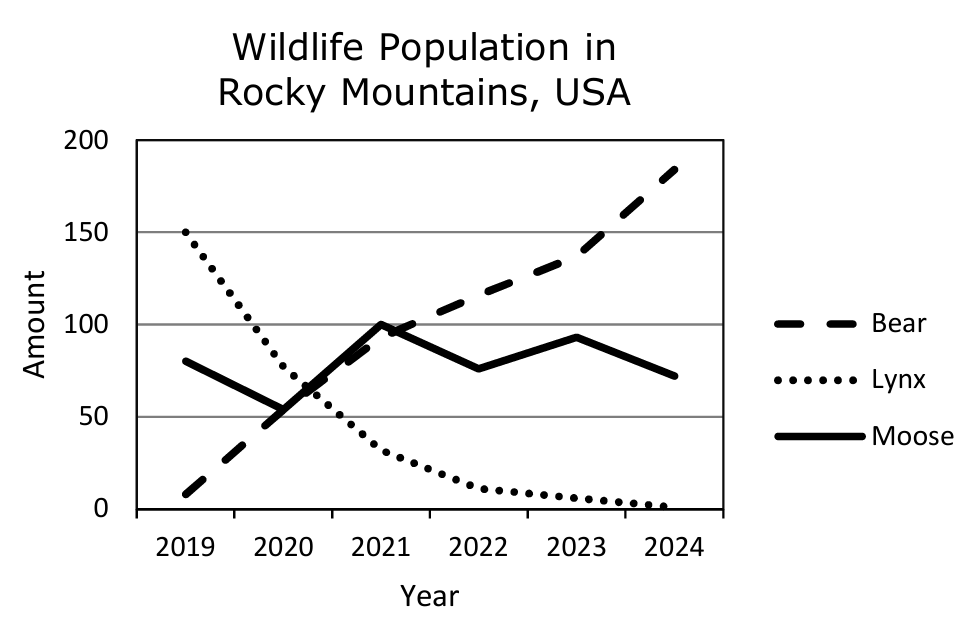
(5.) Number 5

Use the graph above to tick (✓) the incorrect statement:

The bear population has increased over the past five years.

The lynx population rose sharply, and the lynx is frequently sighted in the Rocky Mountains.

The moose population remained relatively stable during the past five years.


From the graph, we notice that the population of lynx decreased exponentially (not rose sharply) from 2019 to 2024
Hence, the incorrect statement is the second one. The second box should be ticked.
(6.) Calculate the simple interest earned on €5000 invested for 4 years at a rate of 3.5% per annum.


$ P = €5000 \\[3ex] r = 3.5\% = \dfrac{3.5}{100} = \dfrac{35}{10 * 100} = \dfrac{35}{1000} \\[5ex] t = 4\;years \\[5ex] SI = P * r * t \\[3ex] = 5000 * \dfrac{35}{1000} * 4 \\[5ex] = 5 * 35 * 4 \\[3ex] = 5 * 4 * 35 \\[3ex] = 20 * 35 \\[3ex] = 2 * 10 * 35 \\[3ex] = 2 * 35 * 10 \\[3ex] = 70 * 10 \\[3ex] = €700 $
(7.) Express 750 as a product of its prime factors.


$ \begin{array}{c} & & 750 \\ & \swarrow & & \searrow \\ \large{\bigcirc} \hspace{-5.5mm} \small{2} & & & & 375 \\ & & & \swarrow & & \searrow \\ & & \large{\bigcirc} \hspace{-5.5mm} \small{3} & & & & 125 \\ & & & & & \swarrow & & \searrow \\ & & & & \large{\bigcirc} \hspace{-5.5mm} \small{5} & & & & 25 \\ & & & & & & & \swarrow & & \searrow \\ & & & & & & \large{\bigcirc} \hspace{-5.5mm} \small{5} & & & & \large{\bigcirc} \hspace{-5.5mm} \small{5} \\ \end{array} \\ 750 = 2 * 3 * 5 * 5 * 5 $
(8.) The function f is defined as $f(x) = \sqrt{x - 6}$.
Find the inverse function $f^{-1}(x)$


$ f(x) = \sqrt{x - 6} \\[3ex] y = \sqrt{x - 6} \\[3ex] \text{Interchange x and y} \\[3ex] x = \sqrt{y - 6} \\[3ex] \text{Solve for y} \\[3ex] \sqrt{y - 6} = x \\[3ex] y - 6 = x^2 \\[4ex] y = x^2 + 6 \\[4ex] \implies \\[3ex] f^{-1}(x) = x^2 + 6 $
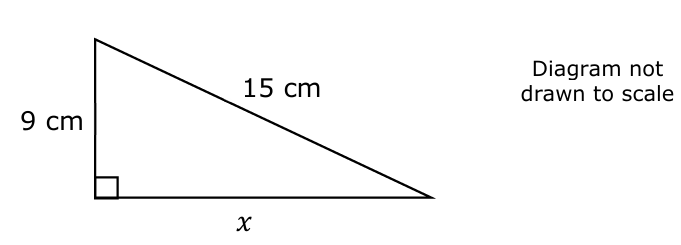
(9.) Work out the value of 𝑥 and the area of the triangle.

Number 9


$ 15^2 = 9^2 + x^2 ...Pythagorean\;\;Theorem \\[4ex] 225 = 81 + x^2 \\[4ex] x^2 + 81 = 225 \\[4ex] x^2 = 225 - 81 \\[4ex] x^2 = 144 \\[4ex] x = \sqrt{144} \\[3ex] x = 12\;cm \\[5ex] \text{Area of the triangle} = \dfrac{1}{2} * \;base\; * \perp height \\[5ex] base = x = 12\;cm \\[3ex] \perp height = 9\;cm \\[3ex] \implies \\[3ex] Area = \dfrac{1}{2} * 12 * 9 \\[5ex] = 6 * 9 \\[3ex] = 54\;cm^2 $
(10.) The volume of a cube is 125 000 cm³.
Work out the length of one side of the cube.


$ \text{Side Length of the cube} = L^3 \\[4ex] Volume = L^3 = 125000\;cm^3 \\[4ex] Volume = 125000\;cm^3 \\[4ex] \implies \\[3ex] L^3 = 125000 \\[4ex] L = \sqrt[3]{125000} \\[3ex] L = 50\;cm $
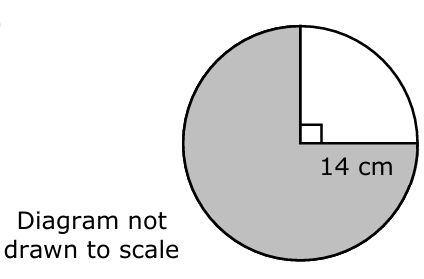
(11.) This is a circle of radius 14 cm.
Work out the area of the shaded part.
(Take π as $\dfrac{22}{7}$)

Number 11


$ radius,\;r = 14\;cm \\[3ex] Area,\;A = \pi r^2 \\[4ex] = \dfrac{22}{7} * 14 * 14 \\[5ex] = 22 * 2 * 14 \\[5ex] \text{Area of shaded part} = \dfrac{3}{4} * A \\[5ex] = \dfrac{3}{4} * 22 * 2 * 14 \\[5ex] = 3 * 22 * 7 \\[3ex] = 66 * 7 \\[3ex] = 462\;cm^2 $
(12.) Work out, giving your answer in standard form:

$ \left(5 * 10^4\right) \div \left(2 * 10^{-2}\right) $


$ \left(5 * 10^4\right) \div \left(2 * 10^{-2}\right) \\[4ex] \dfrac{5 * 10^4}{2 * 10^{-2}} \\[6ex] \dfrac{5}{2} * \dfrac{10^4}{10^{-2}} \\[6ex] 2.5 * 10^{4 - (-2)} \\[4ex] 2.5 * 10^{4 + 2} \\[4ex] 2.5 * 10^6 $
(13.) Evaluate: $8^{-\dfrac{2}{3}}$


$ 8^{-\dfrac{2}{3}} \\[6ex] = \left(\sqrt[3]{8}\right)^{-2}...Law\;7...Exp \\[6ex] = 2^{-2} \\[4ex] = \dfrac{1}{2^2}...Law\;6...Exp \\[6ex] = \dfrac{1}{4} $
(14.) Work out: $\sqrt{1\dfrac{11}{25}}$


$ \sqrt{1\dfrac{11}{25}} \\[6ex] \sqrt{\dfrac{36}{25}} \\[6ex] \dfrac{\sqrt{36}}{\sqrt{25}} \\[6ex] \dfrac{6}{5} \\[5ex] 1\dfrac{1}{5} $
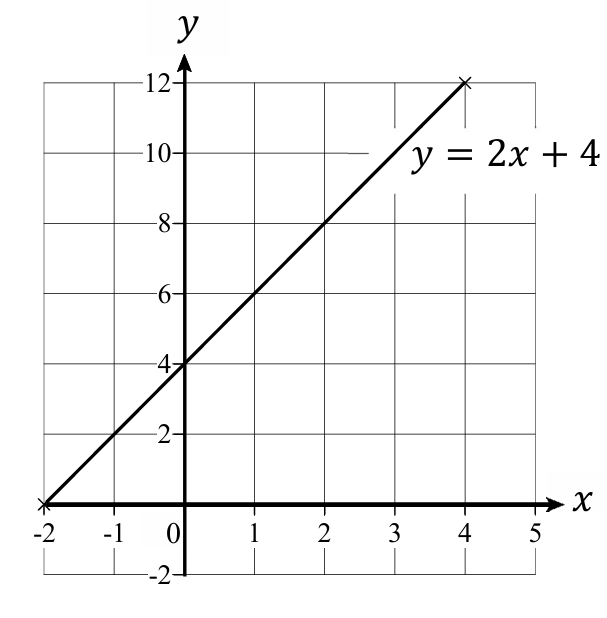
(15.) Number 15

Use the grid above to solve the simultaneous equations: $y = 2x + 4$ and $y = 6$


$ y = 2x + 4...eqn.(1) \\[3ex] y = 6 ...eqn.(2) \\[3ex] y = y \implies eqn.(1) = eqn.(2) \\[3ex] 2x + 4 = 6 \\[3ex] 2x = 6 - 4 \\[3ex] 2x = 2 \\[3ex] x = \dfrac{2}{2} \\[5ex] x = 1 \\[3ex] \therefore x = 1;\;\;y = 6 \\[5ex] \underline{Check} \\[3ex] 2x + 4 \\[3ex] 2(1) + 4 \\[3ex] 2 + 4 \\[3ex] 6 $
(16.) One euro (€) is equivalent to 1.63 Australian Dollars ($)
How many Australian Dollars ($) are obtained for €3000?


$ €1 = 1.63\;A\$ \\[3ex] €3000 = ? \\[5ex] 1 * 3000 = 3000 \\[3ex] Similarly: \\[3ex] 1.63 * 3000 \\[3ex] 1.63 * 3 * 1000 \\[3ex] 1.63 * 1000 * 3 \\[3ex] 1630 * 3 \\[3ex] 4890\;A\$ $
(17.) Fill in the missing spaces:

$ x(2x^2 - ....... + 5) = ....... - 3x^2 + 5x \\[4ex] $

$ x(2x^2 - ....... + 5) = ....... - 3x^2 + 5x \\[4ex] \text{Assume A and B respectively to be the missing spaces} \\[3ex] x(2x^2 - A + 5) = B - 3x^2 + 5x \\[4ex] x(2x^2) = 2x^3 \\[4ex] \implies B = 2x^3 \\[4ex] Also: \\[3ex] x(-A) = -Ax \\[3ex] -Ax = -3x^2 \\[4ex] A = \dfrac{-3x^2}{-x} \\[6ex] A = 3x \\[5ex] \text{The complete equations are:} \\[3ex] LHS:\;\; x(2x^2 - 3x + 5) \\[3ex] RHS:\;\; 2x^3 - 3x^2 + 5x $
(18.) The nth term of a sequence is 7 − 3n
Which term is equal to −68?


Let the nth term = T(n)

$ T(n) = 7 - 3n \\[3ex] T(n) = -68 \\[3ex] \implies \\[3ex] -68 = 7 - 3n \\[3ex] 3n = 7 + 68 \\[3ex] 3n = 75 \\[3ex] n = \dfrac{75}{3} \\[5ex] n = 25 $
(19.) Simplify: $\dfrac{21x^5}{7x^2}$


$ \dfrac{21x^5}{7x^2} \\[6ex] = \dfrac{21}{7} * \dfrac{x^5}{x^2} \\[6ex] 3 * x^{5 - 2} \\[4ex] = 3x^3 $
(20.) Work out the value of: 7.5 × 18.8 + 1.2 × 7.5


$ 7.5 * 18.8 + 1.2 * 7.5 \\[3ex] 141 + 9 \\[3ex] 150 $




Top




(1.)


(2.)


(3.)


(4.)


(5.)


(6.)


(7.)


(8.)


(9.)


(10.)


(11.)


(12.)


(13.)


(14.)


(15.)


(16.)


(17.)


(18.)


(19.)


(20.)


Cash App: Your donation is appreciated. PayPal: Your donation is appreciated. YouTube: Please Subscribe, Share, and Like my Channel
© 2025 Exams Success Group: Your Success in Exams is Our Priority
The Joy of a Teacher is the Success of his Students.