Circle Theorems
Welcome to Our Site
I greet you this day,
These are the solutions to the NZQA past questions on Circle Theorems.
The link to the video solutions will be provided for you. Please subscribe to the YouTube channel to be notified
of upcoming livestreams.
You are welcome to ask questions during the video livestreams.
If you find these resources valuable and if any of these resources were helpful in your passing the
Mathematics papers of the NZQA, please consider making a donation:
Cash App: $ExamsSuccess or
cash.app/ExamsSuccess
PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess
Google charges me for the hosting of this website and my other
educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well.
As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.
Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.
Length of Arc, Area of Sector, Area of Circle, Circumference of Circle
Except stated otherwise, use:
$
d = diameter \\[3ex]
r = radius \\[3ex]
L = arc\:\:length \\[3ex]
A = area\;\;of\;\;sector \\[3ex]
\theta = central\:\:angle \\[3ex]
\pi = \dfrac{22}{7} \\[5ex]
RAD = radians \\[3ex]
^\circ = DEG = degrees \\[7ex]
\boldsymbol{\underline{\theta\;\;in\;\;DEG}} \\[3ex]
L = \dfrac{2\pi r\theta}{360} \\[5ex]
\theta = \dfrac{180L}{\pi r} \\[5ex]
r = \dfrac{180L}{\pi \theta} \\[5ex]
A = \dfrac{\pi r^2\theta}{360} \\[5ex]
\theta = \dfrac{360A}{\pi r^2} \\[5ex]
r = \dfrac{360A}{\pi\theta} \\[7ex]
\underline{Sector\;\;of\;\;a\;\;Circle} \\[3ex]
P = L + 2r \\[3ex]
P = \dfrac{2\pi r\theta}{360} + 2r \\[5ex]
\dfrac{2\pi r\theta}{360} = P - 2r \\[5ex]
\dfrac{\theta}{360} = \dfrac{P - 2r}{2\pi r} \\[5ex]
A = \dfrac{\pi r^2\theta}{360} \\[5ex]
\dfrac{\theta}{360} = \dfrac{A}{\pi r^2} \\[5ex]
\underline{Relationship\;\;Between\;\;P\;\;and\;\;A} \\[3ex]
P = \dfrac{2\pi r\theta}{360} + 2r \\[5ex]
P = 2\pi r \cdot \dfrac{\theta}{360} + 2r \\[5ex]
Substitute\;\;for\;\;\dfrac{\theta}{360} \\[5ex]
P = 2\pi r \left(\dfrac{A}{\pi r^2}\right) + 2r \\[5ex]
P = \dfrac{2A}{r} + \dfrac{2r}{1} \\[5ex]
P = \dfrac{2A + 2r^2}{r} \\[5ex]
P = \dfrac{2(A + r^2)}{r} \\[5ex]
\underline{Relationship\;\;Between\;\;A\;\;and\;\;P} \\[3ex]
A = \dfrac{\pi r^2\theta}{360} \\[5ex]
A = \pi r^2 \cdot \dfrac{\theta}{360} \\[5ex]
Substitute\;\;for\;\;\dfrac{\theta}{360} \\[5ex]
A =\pi r^2 \cdot \dfrac{P - 2r}{2\pi r} \\[5ex]
A = \dfrac{r(P - 2r)}{2} \\[7ex]
\underline{Area\;\;of\;\;Minor\;\;Segment} \\[3ex]
Area\;\;of\;\;Minor\;\;Segment = Area\;\;of\;\;Minor\;\;Sector - Area\;\;of\;\;\triangle \\[3ex]
= \dfrac{\pi r^2\theta}{360} - \dfrac{1}{2}r^2\sin\theta \\[5ex]
= \dfrac{\pi r^2\theta}{360} - \dfrac{r^2\sin\theta}{2} \\[5ex]
= \dfrac{\pi r^2 \theta - 180r^2\sin\theta}{360} \\[5ex]
= \dfrac{r^2(\pi\theta - 180\sin\theta)}{360} \\[7ex]
\boldsymbol{\underline{\theta\;\;in\;\;RAD}} \\[3ex]
L = r\theta \\[5ex]
\theta = \dfrac{L}{r} \\[5ex]
r = \dfrac{L}{\theta} \\[5ex]
A = \dfrac{r^2\theta}{2} \\[5ex]
\theta = \dfrac{2A}{r^2} \\[5ex]
r = \sqrt{\dfrac{2A}{\theta}} \\[7ex]
Circumference\:\:of\:\:a\:\:circle = 2\pi r = \pi d \\[3ex]
L = \dfrac{2A}{r} \\[5ex]
r = \dfrac{2A}{L} \\[5ex]
A = \dfrac{Lr}{2}
$
Circle Theorems
(1.) The angle in a semicircle is a right angle (an angle of 90°).
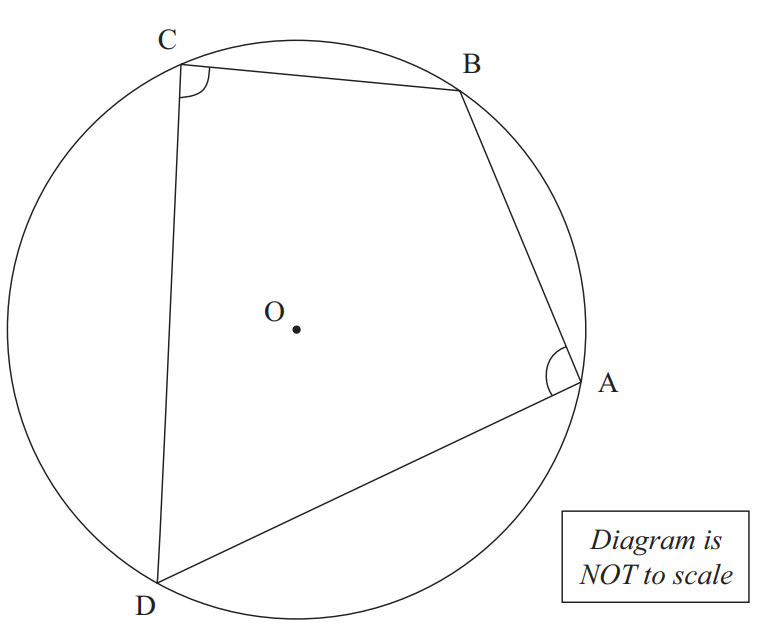
(2.) Angles in the same segment of a circle are equal.
OR
Angles subtended by a chord of a circle in the same segment of the circle are equal.
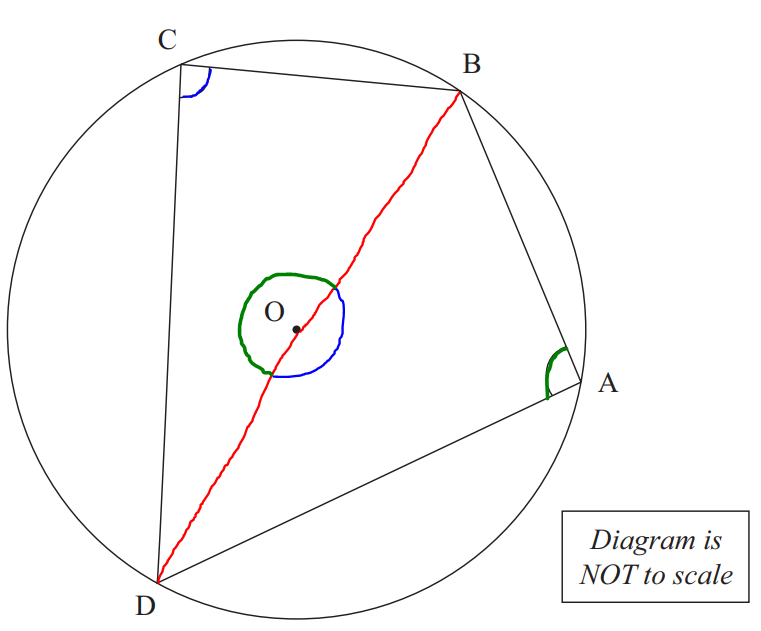
(3.) The angle which an arc of a circle subtends at the center is twice the angle which the same
arc of the circle subtends at the circumference.
OR
The measure of any angle inscribed in a circle is half the measure of the intercepted arc.
(4.) The sum of the interior opposite angles of a cyclic quadrilateral is 180°
OR
The interior opposite angles of a cyclic quadrilateral are supplementary
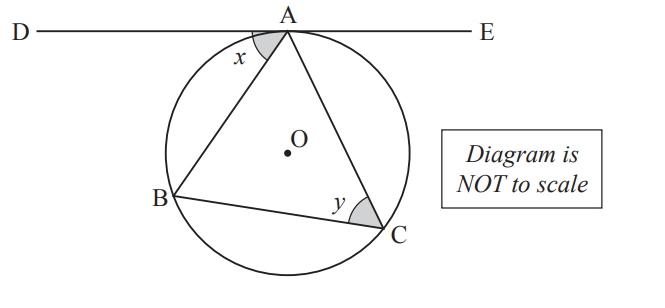
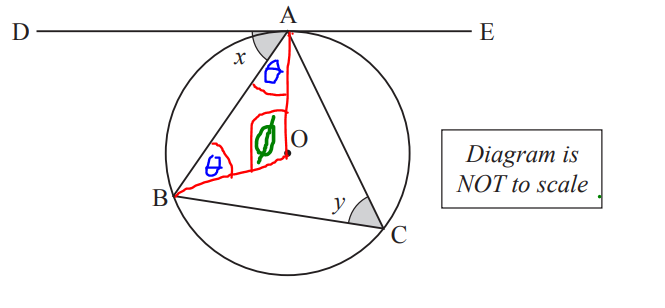
(5.) The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
(6.) The radius of a circle is perpendicular to the tangent of the circle at the point of contact.
This implies that the angle between the radius of a circle and the tangent to the circle at the point of
contact is 90°
(7.) Intersecting Tangents Theorem or Intersecting Tangent-Tangent Theorem and
Angle of Intersecting Tangents Theorem
If two tangents are drawn from the same external point:
(a.) the two tangents are equal in length
(b.) the line joining the external point and the centre of the circle bisects the angle formed by the two
tangents.
(c.) the line joining the external point and the centre of the circle bisects the angle formed by the two
radii.
(8.) Alternate Segment Theorem
The angle between a tangent to a circle and a chord drawn from the point of contact, is equal to the angle in
the alternate segment.
(9.) If a line drawn from the center of the circle bisects a chord, then:
(a.) it bisects its arc (the angle opposite the chord) and
(b.) it is perpendicular to the chord.
(10.) If a line drawn from the center of the circle is perpendicular to a chord, then:
(a.) it bisects the chord and
(b.) it bisects its arc (the angle opposite the chord).
(11.) Intersecting Chords Theorem
When two chords intersect, the product of the lengths of the segments of one chord is equal to the product of
the
lengths of the segments of the other chord.
(12.) Angle of Intersecting Chords Theorem
The angle formed when two chords intersect is equal to half the sum of the intercepted arcs.
(13.) Intersecting Secants Theorem or Intersecting Secant-Secant Theorem
In the intersection of two secants from the same external point:
the product of the distance between the first point and the external point and the distance between the
second point and the external point for the first secant is equal to
the product of the distance between the first point and the external point and the distance between the
second point and the external point for the second secant.
(14.) Angle of Intersecting Secants (Inside the Circle) Theorem
The angle formed when two secants intersect inside a circle is equal to half the sum of the intercepted arcs.
(15.) Angle of Intersecting Secants (Outside the Circle) Theorem
The angle formed when two secants intersect outside a circle is equal to half the difference of the
intercepted arcs.
(16.) Intersecting Secant-Tangent Theorem or Intersecting Tangent-Secant Theorem
In the intersection of a secant and a tangent from the same external point:
the product of the distance between the first point and the external point and the distance between the
second point and the external point for the secant is equal to
the square of the distance between the point of contant and the external point for the tangent.
(17.) Angle of Intersecting Secant-Tangent Theorem
The angle formed when a secant and a tangent intersect outside a circle is equal to half the difference of the
intercepted arcs.
Give geometric reasons for each step in your solution.
Construction: Join the radii: from the centre O to point B, and from the centre O to point D
$ \color{blue}{\angle DOB} = 2 * \angle DCB ...\text{angle at center = 2 times the angle at circumference} \\[3ex] \color{green}{\angle DOB} = 2 * \angle DAB ...\text{angle at center = 2 times the angle at circumference} \\[3ex] \color{blue}{\angle DOB} + \color{green}{\angle DOB} = 360^\circ ...\text{angles at a point} \\[3ex] \implies \\[3ex] 2 * \angle DCB + 2 * \angle DAB = 360 \\[3ex] 2(\angle DCB + \angle DAB) = 360 \\[3ex] \angle DCB + \angle DAB = \dfrac{360}{2} \\[5ex] \angle DCB + \angle DAB = 180^\circ \\[3ex] \angle DCB = \angle C ...diagram \\[3ex] \angle DAB = \angle A ...diagram \\[3ex] \implies \\[3ex] \angle C + \angle A = 180^\circ $
O is the centre of the circle.
DE is a tangent to the circle.
Point A is where DE touches the circle.
Prove that angle x equal angle y.
Justify your answer with clear geometric reasoning.
Construction: Join the radii: from centre O to the point A, and from centre O to point B
Radii: |OA| and |OB|
This forms a triangle.
Label the angles in the triangle.
$ \angle OAB = \theta \\[3ex] \angle OBA = \theta \\[3ex] \angle AOB = \phi \\[5ex] \angle OAB = \angle OBA = \theta ...base\;\;\angle s\;\;of\;\;isosceles\;\;\triangle AOB \\[3ex] \theta + \theta + \phi = 180^\circ ...sum\;\;of\;\;\angle s\;\;of\;\;\triangle AOB \\[3ex] 2\theta + \phi = 180 ...eqn.(1) \\[5ex] \theta + x = 90^\circ ...radius\;OA \perp tangent\;DAE\;\;at\;\;point\;\;contact\;A \\[3ex] \theta + x = 90 ...eqn.(2) \\[3ex] \implies \\[3ex] \theta = 90 - x ...eqn.(3) \\[5ex] \phi = 2 * y ...\angle \;\;at\;\;centre = 2 * \angle \;\;at\;\;circumference \\[3ex] \phi = 2y ...eqn.(4) \\[5ex] Substitute\;\;eqn.(3)\;\;and\;\;eqn.(4)\;\;into\;\;eqn.(1) \\[3ex] 2\theta + \phi = 180 \\[3ex] 2(90 - x) + 2y = 180 \\[3ex] 180 - 2x + 2y = 180 \\[3ex] 2y = 180 - 180 + 2x \\[3ex] 2y = 2x \\[3ex] Divide\;\;both\;\;sides\;\;by\;\;2 \\[3ex] y = x \\[3ex] x = y \\[3ex] $ Therefore, the angle between the tangent DAE and the chord AB (the angle is x) is equal to the angle in the alternate segment (the angle is y)
