Exponents and Logarithms

Welcome to Our Site

I greet you this day,
These are the solutions to the NZQA past questions on the topics: Exponents and Logarithms.
When applicable, the TI-84 Plus CE calculator (also applicable to TI-84 Plus calculator) solutions are provided for some questions.
The link to the video solutions will be provided for you. Please subscribe to the YouTube channel to be notified of upcoming livestreams. You are welcome to ask questions during the video livestreams.
If you find these resources valuable and helpful in your passing the Mathematics exam of the NZQA, please consider making a donation:

Cash App: $ExamsSuccess or
cash.app/ExamsSuccess

PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess

Google charges me for the hosting of this website and my other educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well. As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.

Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.

These are the notable notes regarding factoring

Factoring Formulas

$ \underline{Difference\;\;of\;\;Two\;\;Squares} \\[3ex] (1.)\;\;x^2 - y^2 = (x + y)(x - y) \\[5ex] \underline{Difference\;\;of\;\;Two\;\;Cubes} \\[3ex] (2.)\;\; x^3 - y^3 = (x - y)(x^2 + xy + y^2) \\[5ex] \underline{Sum\;\;of\;\;Two\;\;Cubes} \\[3ex] (3.)\;\; x^3 + y^3 = (x + y)(x^2 - xy + y^2) $

Laws of Exponents and Laws of Logarithms (Math)

Law 1: Exponents
(1.) Product Rule

$ p^c * p^d = p^{c + d} \\[4ex] p^{c + d} = p^c * p^d $

Law 1: Logarithms
(1.)

$ \log_p{c} + \log_p{d} = \log_p{cd} \\[4ex] \log_p{cd} = \log_p{c} + \log_p{d} $

Law 2: Exponents
(2.) Quotient Rule

$ p^c \div p^d = p^{c - d} \\[4ex] \dfrac{p^c}{p^d} = p^{c - d} \\[4ex] p^{c - d} = p^c \div p^d \\[4ex] p^{c - d} = \dfrac{p^c}{p^d} $

Law 2: Logarithms
(2.)

$ \log_p{c} - \log_p{d} = \log_p({c \div d}) \\[4ex] \log_p{c} - \log_p{d} = \log_p{\left(\dfrac{c}{d}\right)} \\[5ex] \log_p({c \div d}) = \log_p{c} - \log_p{d} \\[4ex] \log_p{\left(\dfrac{c}{d}\right)} = \log_p{c} - \log_p{d} $

Law 3: Exponents
(3.)

$ {any\: base}^0 = 1 \\[5ex] p^0 = 1 $

Law 3: Logarithms
(3.)

$ \log_{any\: base}{1} = 0 \\[5ex] \log_p{1} = 0 \\[4ex] \ln{1} = \log_e{1} = 0 $

Law 4: Exponents
(4.)

$ {any\: base}^1 = any\: base \\[5ex] p^1 = p $

Law 4: Logarithms
(4.)

$ \log_{any\: base}{any\: base} = 1 \\[5ex] \log_p{p} = 1 $

Law 5: Exponents
(5.) Expanded Power Rule

$ (p)^c = (p^1)^c = p^{1 * c} = p^c \\[5ex] \left(\dfrac{p}{q}\right)^c = \dfrac{p^c}{q^c} \\[7ex] (p^c)^d = p^{c * d} \\[5ex] p^{c * d} = (p^c)^d \\[7ex] \left(\dfrac{p^c}{q^d}\right)^e = \dfrac{p^{ce}}{q^{de}} \\[7ex] (pk)^d = p^d * k^d \\[5ex] p^d * k^d = (pk)^d \\[5ex] (p^c k^d)^m = p^{cm} * k^{dm} \\[5ex] p^{cm} * k^{dm} = (p^c)^m * (k^d)^m = (p^c k^d)^m \\[5ex] (p^c)^{\dfrac{d}{e}} = p^{\dfrac{cd}{e}} \\[7ex] p^{\dfrac{cd}{e}} = (p^c)^{\dfrac{d}{e}} $

Law 5: Logarithms
(5.)

$ \log_p{c^d} = d * \log_p{c} \\[4ex] d * \log_p{c} = \log_p{c^d} $

Law 6: Exponents
(6.) Rule of Negative Exponents

$ p^{-c} = \dfrac{1}{p^c} \\[5ex] \dfrac{1}{p^c} = p^{-c} \\[5ex] p^c = \dfrac{1}{p^{-c}} \\[5ex] \dfrac{1}{p^{-c}} = p^c \\[5ex] p^{-\dfrac{c}{d}} = \dfrac{1}{p^{\dfrac{c}{d}}} \\[7ex] \dfrac{1}{p^{\dfrac{c}{d}}} = p^{-\dfrac{c}{d}} \\[7ex] p^{\dfrac{c}{d}} = \dfrac{1}{p^{-\dfrac{c}{d}}} \\[7ex] \dfrac{1}{p^{-\dfrac{c}{d}}} = p^{\dfrac{c}{d}} $

Law 6: Logarithms
(6.)
Change of Base of Log

$ \log_p{d} = \dfrac{\log_c{d}}{\log_c{p}} \\[4ex] \dfrac{\log_c{d}}{\log_c{p}} = \log_p{d} \\[4ex] \log_p{d} * \log_c{p} = \log_c{d} \\[4ex] \log_c{d} = \log_p{d} * \log_c{p} $

Law 7: Exponents
(7.) Rule of Fractional Exponents

$ p^{\dfrac{1}{c}} = \sqrt[c]{p} \\[5ex] p^{\dfrac{c}{d}} = \sqrt[d]{p^c} \\[5ex] p^{\dfrac{c}{d}} = (\sqrt[d]{p})^c \\[5ex] \sqrt[d]{p^c} = p^{\dfrac{c}{d}} \\[5ex] (\sqrt[d]{p})^c = p^{\dfrac{c}{d}} $

Law 7: Logarithms
(7.)

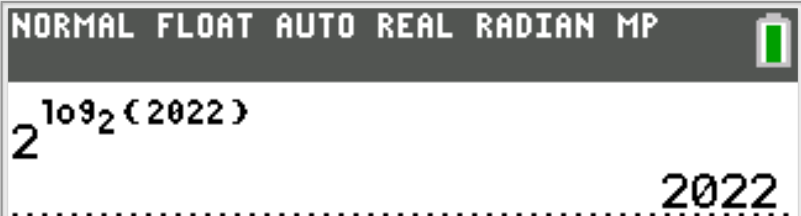
$ p^{\log_p{c}} = c \\[5ex] c = p^{\log_p{c}} \\[5ex] p^{d\log_p{c}} = p^{\log_p{c^d}} = c^d \\[5ex] c^d = p^{\log_p{c^d}} = p^{d\log_p{c}} \\[5ex] e^{\ln{c}} = c \\[5ex] c = e^{\ln{c}} \\[5ex] e^{d\ln{c}} = e^{\ln{c^d}} = c^d \\[5ex] c^d = e^{\ln{c^d}} = e^{d\ln{c}} $

Laws of Exponents

Law 1:
If two or more expressions have: the same base, and are being multiplied;
Keep the base
Add the exponents.

Law 2:
If two expressions have: the same base, and are being divided;
Keep the base
Subtract the exponents.
Subtracting the exponents means subtract the exponent of the denominator from the exponent of the numerator.

Law 3:
Any base raised to an exponent of $0$ gives a result of $1$
In other words, the result of any base raised to an exponent of 0, is 1

Law 4:
Any base raised to an exponent of $1$ is that base.
In other words, the result of any base raised to an exponent of 1, is that base.

Law 5:
If an expression, having one base enclosed in parenthesis, has two exponents: an inner exponent and an outer exponent;
Keep the base
Multiply the exponents.
If an expression, having a product of multiple bases enclosed in parenthesis, has two exponents: an inner exponent and an outer exponent;
Keep each base as a product
Multiply the exponents.

Law 6:
A base with a negative exponent is the reciprocal of the same base with the corresponding positive exponent.
A base with a positive exponent is the reciprocal of the same base with the corresponding negative exponent.

Law 7:
Fractional exponents leads to radicals.
In other words, a base whose exponent is a fraction can be expressed as a radical.

Laws of Logarithms

Law 1:
If two logarithms have: the same base, and are being added;
Keep the base
Multiply the numbers.

Law 2:
If two logarithms have: the same base, and are being subtracted;
Keep the base
Divide the numbers.

Law 3:
The logarithm of the number, 1; to any base gives a result of 0
In other words, the result of the logarithm of 1; to any base is 0

Law 4:
The logarithm of a number; to that number as the base, gives a result of 1
In other words, the result of the logarithm of a number to that same number as the base is 1

Law 5:
The logarithm of a number to a base, raised to an exponent; is equal to the exponent times the logarithm of that number to the base.

Law 6:
This Law deals with the Change of Base of Logarithms.
Any logarithm of a number to a base, can be expressed as a ratio of two logarithms to another base.
Say you have the logarithm of a number say $d$ to a base, say p; and
You want to change the base of that logarithm to another base, say c; then the logarithm of d to base p is the logarithm of d to base c divided by the logarithm of p to base c.
In other words, the logarithm of d to base p is the ratio of the logarithm of d to base c, to the logarithm of p to base c.

Law 7:
This Law actually deals with both exponents and logarithms.
The result of a base, raised to an exponent of the logarithm of a number whose base is the base, is the number.

(1.) Solve the equation $2^x = 2022$

$ 2^x = 2022 \\[3ex] Introduce\;\;\log\;\;to\;\;both\;\;sides \\[3ex] \log 2^x = \log 2022 \\[3ex] x\log 2 = \log 2022 ...Law\;5\;Log \\[3ex] x = \dfrac{\log 2022}{\log 2} \\[5ex] x = \log_{2}2022...Law\;6\;Log \\[4ex] $ Check

$ x = \log_{2}2022 $
LHS	RHS
$ 2^x \\[3ex] 2^{\log_{2}2022} \\[5ex] 2022 ...Law\;7\;Log $	$2022$

(4.) If $\log_b{x} = 2$ and $\log_{3b}{y} = 2$, write y in terms of x.

$ \log_b{x} = 2 \\[4ex] b^2 = x ...Exponent-Logarithm\;\;Relationship \\[3ex] x = b^2 \\[3ex] \log_{3b}{y} = 2 \\[4ex] (3b)^2 = y ...Exponent-Logarithm\;\;Relationship \\[3ex] y = (3b)^2 \\[3ex] y = 3^2 \cdot b^2 \\[3ex] y = 9 \cdot x \\[3ex] y = 9x $

(5.) Solve $9^{(2x + 3)} = \left(\dfrac{1}{27}\right)^x$

$ 9^{(2x + 3)} = \left(\dfrac{1}{27}\right)^x \\[5ex] 9^{2x + 3} = \left(27^{-1}\right)^x...Law\;6\;Exp \\[4ex] 3^{2(2x + 3)} = \left[\left(3^3\right)^{-1}\right]^x \\[4ex] 3^{4x + 6} = 3^{-3x} ...Law\;5\;Exp \\[4ex] Same\;\;Base;\;\;Equate\;\;Exponents \\[3ex] 4x + 6 = -3x \\[3ex] 4x + 3x = -6 \\[3ex] 7x = -6 \\[3ex] x = -\dfrac{6}{7} \\[5ex] $ Check

$ x = -\dfrac{6}{7} $
LHS	RHS
$ 9^{(2x + 3)} \\[3ex] 2x + 3 = 2\left(-\dfrac{6}{7}\right) + 3 \\[5ex] = -\dfrac{12}{7} + \dfrac{21}{7} \\[5ex] = \dfrac{9}{7} \\[5ex] \implies \\[3ex] 9^{\dfrac{9}{7}} \\[7ex] 3^{2\left(\dfrac{9}{7}\right)} \\[7ex] 3^{\dfrac{18}{7}} $	$ \left(\dfrac{1}{27}\right)^x \\[5ex] \left(27^{-1}\right)^x \\[4ex] \left[\left(3^3\right)^{-1}\right]^x \\[4ex] 3^{-3x} \\[4ex] 3^{-3\left(-\dfrac{6}{7}\right)} \\[7ex] 3^{\dfrac{18}{7}} $

(6.) Simplify each expression, leaving your answer with positive indices.

$ (i.) \dfrac{(3y)^4}{3y^{-1}} \\[5ex] (ii.) \sqrt[3]{8y^{27}} \\[5ex] $

$ (i.) \\[3ex] \dfrac{(3y)^4}{3y^{-1}} \\[7ex] \dfrac{3^4 \cdot y^4}{3^1 \cdot y^{-1}} ...Law\;5...Exp \\[7ex] 3^{4 - 1} \cdot y^{4 -(-1)} ...Law\;5...Exp \\[4ex] 3^3 \cdot y^{4 + 1} \\[4ex] 27 \cdot y^{5} \\[4ex] 27y^5 \\[5ex] (ii.) \\[3ex] \sqrt[3]{8y^{27}} \\[4ex] \sqrt[3]{8} \cdot \sqrt[3]{y^{27}} \\[4ex] 2 \cdot \left(y^{27}\right)^{\dfrac{1}{3}} ...Law\;7...Exp \\[7ex] 2 \cdot y^9 \\[4ex] 2y^9 $

(7.) Consider the equation $\log_2(x - a) - \log_2(x + a) = c$, where a and c are constants.

(i.) Show that when x is made the subject of this equation, $x = a \dfrac{1 + 2^c}{1 - 2^c}$
Ensure that you use correct mathematical statements in your reasoning.

(ii.) The equation $\log_2(x - a) - \log_2(x + a) = c$ is only possible to solve for some values of a and for some values of c.
Explaining your reasoning clearly, describe which values of a and of c will make the equation possible to solve.
You may find it useful to recall that, when x is made the subject of this equation, $x = a \dfrac{1 + 2^c}{1 - 2^c}$

$ (i.) \\[3ex] \log_2(x - a) - \log_2(x + a) = c \\[3ex] \log_2\left[\dfrac{x - a}{x + a}\right] = c ...Law\;2\;Log \\[5ex] \dfrac{x - a}{x + a} = 2^c ...Relationship\;\;Between\;\;Exp\;\;and\;\;Log \\[5ex] x - a = 2^c(x + a) \\[4ex] x - a = x \cdot 2^c + a \cdot 2^c \\[4ex] x - x \cdot 2^c = a \cdot 2^c + a \\[4ex] x(1 - 2^c) = a(2^c + 1) \\[4ex] x(1 - 2^c) = a(1 + 2^c) \\[4ex] x = \dfrac{a(1 + 2^c)}{1 - 2^c} \\[5ex] $ Let us begin by testing for some values of a
Then, we shall test for some values of c

$ (ii.) \\[3ex] \log_2(x - a) - \log_2(x + a) = c \\[3ex] Assume\;\;a = 0 \\[3ex] \log_2(x - 0) - \log_2(x + 0) = c \\[3ex] \log_2{x} - \log_2{x} = c \\[3ex] 0 = c \\[3ex] c = 0 \\[3ex] $ So, when a = 0, c = 0
But we do not have any x, so this is an issue.
Also:

$ \log_2(x - a) - \log_2(x + a) = c \\[3ex] Assume\;\;c = 0 \\[3ex] \log_2(x - a) - \log_2(x + a) = 0 \\[3ex] \log_2\left[\dfrac{x - a}{x + a}\right] = 0 \\[5ex] \dfrac{x - a}{x + a} = 2^0 \\[5ex] \dfrac{x - a}{x + a} = 1 \\[5ex] x - a = x + a \\[3ex] 0 = 2a \\[3ex] 2a = 0 \\[3ex] a = \dfrac{0}{2} \\[5ex] a = 0 \\[3ex] $ So, when c = 0, a = 0
But we do not have any x, so this is an issue.
So, for us to solve for x, a ≠ 0 and c ≠ 0

If we decide to use this formula:

$ x = \dfrac{a(1 + 2^c)}{1 - 2^c} \\[5ex] Denominator \ne 0 ...to\;\;make\;\;it\;\;defined \\[3ex] Assume\;\;we\;\;set\;\;it\;\;to\;\;0 \\[3ex] 1 - 2^c = 0 \\[4ex] 1 = 2^c \\[4ex] 2^c = 1 \\[4ex] 2^c = 2^0 \\[4ex] c = 0 \\[3ex] $ This implies that c should not be equal to 0.

(8.) The level of sound (intensity) is measured on a logarithmic scale using a unit called a decibel.
The formula for the decibel level, d, is given by $$ d = 10\log_{10}\left(\dfrac{P}{P_0}\right) $$ where P is the intensity of the sound and P₀ is the weakest sound that the human ear can hear.
A cooling fan has a decibel level of 38 decibels.
A heat pump has a decibel level of 30 decibels.
Show that the cooling fan sound intensity is more than six times that of the heat pump sound intensity.

$ d = 10\log_{10}\left(\dfrac{P}{P_0}\right) \\[5ex] \underline{Cooling\;\;Fan} \\[3ex] d = 38\;decibels \\[3ex] P_0 = P_0 \\[3ex] P = P_f \\[3ex] 10\log_{10}\left(\dfrac{P_f}{P_0}\right) = 38 \\[5ex] \log_{10}\left(\dfrac{P_f}{P_0}\right) = \dfrac{38}{10} \\[5ex] \log_{10}\left(\dfrac{P_f}{P_0}\right) = 3.8 \\[5ex] \dfrac{P_f}{P_0} = 10^{3.8} \\[4ex] P_f = P_0 \cdot 10^{3.8} \\[5ex] \underline{Heat\;\;Pump} \\[3ex] d = 30\;decibels \\[3ex] P_0 = P_0 \\[3ex] P = P_h \\[3ex] 10\log_{10}\left(\dfrac{P_h}{P_0}\right) = 30 \\[5ex] \log_{10}\left(\dfrac{P_h}{P_0}\right) = \dfrac{30}{10} \\[5ex] \log_{10}\left(\dfrac{P_h}{P_0}\right) = 3 \\[5ex] \dfrac{P_h}{P_0} = 10^{3} \\[4ex] P_h = P_0 \cdot 10^{3} \\[5ex] Show\;\;that\;\;P_f \gt 6 \cdot P_h \\[3ex] \implies \\[3ex] P_0 \cdot 10^{3.8} \gt 6 \cdot P_0 \cdot 10^{3} \\[4ex] 10^{3.8} \gt 6 \cdot 10^3 \\[4ex] 6309.573445 \gt 6000 $

(9.) Jessica is investigating a compounding investment.
She wants to know how long it would take for an investment of $1000 to double in value to $2000.
She forms the following equation: $$ 2000 = 1000\left(1 + \dfrac{R}{100}\right)^D $$ where R is the rate of return on the investment, as a percentage, and
D is the time that the investment would take to double in value, in years.

(i.) If an investment takes 11 years to double in value, what is the rate of return?
(ii.) By making D the subject of the expression: $2000 = 1000\left(1 + \dfrac{R}{100}\right)^D$, show that $D = \dfrac{\log(2)}{\log\left(1 + \dfrac{R}{100}\right)}$

In her research, Jessica comes across a simple but approximate rule for calculating D, the time that the investment would take to double in value.
It is commonly called the 'Rule of 72', and it states that: $$ D = \dfrac{72}{R} $$ Jessica wonders how close the values of D from the 'Rule of 72' are to those calculated using the actual expression, which is: $$ D = \dfrac{\log(2)}{\log\left(1 + \dfrac{R}{100}\right)} $$ (iii.) Show clearly that the value of R for which the 'Rule of 72' exactly calculates D, is the solution to the equation: $$ 2^R - \left(1 + \dfrac{R}{100}\right)^{72} = 0 $$ You do not need to solve this equation.

$ (i.) \\[3ex] D = 11\;years \\[3ex] 2000 = 1000\left(1 + \dfrac{R}{100}\right)^D \\[5ex] 1000\left(1 + \dfrac{R}{100}\right)^D = 2000 \\[5ex] \left(1 + \dfrac{R}{100}\right)^{11} = \dfrac{2000}{1000} \\[5ex] \left(1 + \dfrac{R}{100}\right)^{11} = 2 \\[5ex] Multiply\;\;the\;\;exponent\;\;on\;\;both\;\;sides\;\;by\;\;\dfrac{1}{11} \\[5ex] \left(1 + \dfrac{R}{100}\right)^{11 \cdot \dfrac{1}{11}} = 2^{\dfrac{1}{11}}...Law\;5...Exp \\[9ex] 1 + \dfrac{R}{100} = 1.065041089 \\[5ex] \dfrac{R}{100} = 1.065041089 - 1 \\[5ex] \dfrac{R}{100} = 0.0650410894 \\[5ex] R = 100(0.0650410894) \\[3ex] R = 6.504108944\% \\[5ex] (ii.) \\[3ex] 2000 = 1000\left(1 + \dfrac{R}{100}\right)^D \\[5ex] 1000\left(1 + \dfrac{R}{100}\right)^D = 2000 \\[5ex] \left(1 + \dfrac{R}{100}\right)^D = \dfrac{2000}{1000} \\[5ex] \left(1 + \dfrac{R}{100}\right)^D = 2 \\[5ex] Introduce\;\;Logarithm\;\;to\;\;both\;\;sides \\[3ex] \log \left(1 + \dfrac{R}{100}\right)^D = \log(2) \\[5ex] D \log \left(1 + \dfrac{R}{100}\right) = \log(2) ...Law\;5...Log \\[5ex] D = \dfrac{\log(2)}{\log\left(1 + \dfrac{R}{100}\right)} \\[10ex] (iii.) \\[3ex] D = \dfrac{72}{R} \\[5ex] D = \dfrac{\log(2)}{\log\left(1 + \dfrac{R}{100}\right)} \\[8ex] D = D \implies \\[3ex] \dfrac{\log(2)}{\log\left(1 + \dfrac{R}{100}\right)} = \dfrac{72}{R} \\[7ex] Cross\;\;Multiply \\[3ex] R\log 2 = 72\log\left(1 + \dfrac{R}{100}\right)^{72} \\[5ex] \log 2^R = \log\left(1 + \dfrac{R}{100}\right)^{72} ...Law\;5...Log \\[5ex] \log 2^R - \log\left(1 + \dfrac{R}{100}\right)^{72} = 0 \\[7ex] \log\left[\dfrac{2^R}{\left(1 + \dfrac{R}{100}\right)^{72}}\right] = 0 ...Law\;2...Log \\[10ex] \log = \log_{10} ...standard\;\;log \\[3ex] \implies \\[3ex] \log_{10}\left[\dfrac{2^R}{\left(1 + \dfrac{R}{100}\right)^{72}}\right] = 0 \\[10ex] 10^0 = \dfrac{2^R}{\left(1 + \dfrac{R}{100}\right)^{72}}...Exponent-Logarithm\;\;Relationship \\[10ex] 1 = \dfrac{2^R}{\left(1 + \dfrac{R}{100}\right)^{72}}...Law\;3...Exp \\[10ex] \dfrac{2^R}{\left(1 + \dfrac{R}{100}\right)^{72}} = 1 \\[10ex] Cross\;\;Multiply \\[3ex] 2^R = \left(1 + \dfrac{R}{100}\right)^{72} \\[5ex] 2^R - \left(1 + \dfrac{R}{100}\right)^{72} = 0 \\[5ex] $

(11.) Simplify each expression, leaving your answer with positive indices.

$ (i.)\;\; \sqrt[5]{\dfrac{4(2n)^3}{n^8}} \\[7ex] (ii.)\;\; \left(\dfrac{n^3}{16n^6}\right)^{-0.5} \\[7ex] $

$ (i.) \\[3ex] \sqrt[5]{\dfrac{4(2n)^3}{n^8}} \\[7ex] \sqrt[5]{\dfrac{4 \cdot 2^3 \cdot n^3}{n^8}} ...Law\;5...Exp \\[7ex] \sqrt[5]{\dfrac{32}{n^{8 - 3}}} ...Law\;2...Exp \\[7ex] \sqrt[5]{\dfrac{32}{n^{5}}} \\[7ex] \dfrac{\sqrt[5]{32}}{\sqrt[5]{n^5}} \\[7ex] \dfrac{2}{n^{5 \cdot \dfrac{1}{5}}} ...Law\;7...Exp \\[7ex] \dfrac{2}{n} \\[7ex] (ii.) \\[3ex] \left(\dfrac{n^3}{16n^6}\right)^{-0.5} \\[7ex] \left(\dfrac{1}{16 \cdot n^{6 - 3}}\right)^{-0.5} ...Law\;2...Exp \\[7ex] \left(\dfrac{1}{16 \cdot n^{3}}\right)^{-0.5} ...Law\;2...Exp \\[7ex] \dfrac{1^{-0.5}}{16^{-0.5} \cdot \left(n^3\right)^{-0.5}} ...Law\;5...Exp \\[10ex] Solving\;\;step\;\;by\;\;step \\[3ex] -0.5 = -\dfrac{5}{10} = -\dfrac{1}{2} \\[5ex] 1^{-0.5} = 1 \\[4ex] 16^{-0.5} = 16^{-\dfrac{1}{2}} = \left(2^4\right)^{-\dfrac{1}{2}} = 2^{-2} ...Law\;5...Exp \\[8ex] \left(n^3\right)^{-0.5} = \left(n^3\right)^{-\dfrac{1}{2}} = n^{-\dfrac{3}{2}} ...Law\;5...Exp \\[8ex] \implies \\[3ex] \dfrac{1}{2^{-2} \cdot n^{-\dfrac{3}{2}}} \\[10ex] \dfrac{1}{2^{-2}} \cdot \dfrac{1}{n^{-\dfrac{3}{2}}} \\[10ex] 2^2 \cdot n^{\dfrac{3}{2}} ...Law\;6...Exp \\[7ex] 4 \cdot \sqrt{n^3} \\[4ex] 4\sqrt{n^3} $

(12.) The value, V, in dollars ($), of a laptop can be modelled by $V = 40 + ke^{-0.5t},\;t \ge 0$, where t is the time in years since the laptop was purchased.
The original price of the laptop was $900.
How long does it takes for the laptop's value to be reduced to 50% of the original value?

$ V = 40 + ke^{-0.5t},\;t \ge 0 \\[4ex] At\;\;original\;\;price, \;\;t = 0 \\[3ex] \implies \\[3ex] 900 = 40 + ke^{-0.5 \cdot 0} \\[4ex] 40 + ke^{0} = 900 \\[3ex] 40 + k(1) = 900 ...Law\;3...Exp \\[3ex] k = 900 - 40 \\[3ex] k = 860 \\[3ex] Value\;\;to\;\;be\;\;reduced\;\;to\;\;50\%\;\;of\;\;the\;\;original\;\;value \\[3ex] 50\%\;\;of\;\;original\;\;price \\[3ex] = 50\%\;\;of\;\;900 \\[3ex] = 0.5(900) \\[3ex] = 450 \\[3ex] \implies \\[3ex] 40 + ke^{-0.5t} = 450 \\[4ex] 40 + 860e^{-0.5t} = 450 \\[4ex] 860e^{-0.5t} = 450 - 40 \\[4ex] 860e^{-0.5t} = 410 \\[4ex] e^{-0.5t} = \dfrac{410}{860} \\[5ex] e^{-0.5t} = \dfrac{41}{86} \\[5ex] Introduce\;\;\ln\;\;to\;\;both\;\;sides \\[3ex] \ln e^{-0.5t} = \ln\left(\dfrac{41}{86}\right) \\[5ex] -0.5t = -0.7407752295 \\[3ex] t = \dfrac{-0.7407752295}{-0.5} \\[5ex] t = 1.481550459\;years $

(13.) Show that $\dfrac{\left[x^{\dfrac{3}{2}} + x^{\dfrac{1}{2}}\right]\left[x^{\dfrac{1}{2}} - x^{\dfrac{-1}{2}}\right]}{\left[x^{\dfrac{3}{2}} - x^{\dfrac{1}{2}}\right]^2}$ can be simplified to $\dfrac{x + 1}{x(x - 1)}$

$ \dfrac{\left[x^{\dfrac{3}{2}} + x^{\dfrac{1}{2}}\right]\left[x^{\dfrac{1}{2}} - x^{\dfrac{-1}{2}}\right]}{\left[x^{\dfrac{3}{2}} - x^{\dfrac{1}{2}}\right]^2} \\[12ex] \dfrac{x^{\dfrac{3}{2}} \cdot x^{\dfrac{1}{2}} - x^{\dfrac{3}{2}} \cdot x^{\dfrac{-1}{2}} + x^{\dfrac{1}{2}} \cdot x^{\dfrac{1}{2}} - x^{\dfrac{1}{2}} \cdot x^{\dfrac{-1}{2}}}{\left[x^{\dfrac{3}{2}} - x^{\dfrac{1}{2}}\right]\left[x^{\dfrac{3}{2}} - x^{\dfrac{1}{2}}\right]} \\[12ex] \dfrac{x^{\dfrac{3}{2} + \dfrac{1}{2}} - x^{\dfrac{3}{2} + \dfrac{-1}{2}} + x^{\dfrac{1}{2} + \dfrac{1}{2}} - x^{\dfrac{1}{2} + \dfrac{-1}{2}}} {x^{\dfrac{3}{2}} \cdot x^{\dfrac{3}{2}} - x^{\dfrac{3}{2}} \cdot x^{\dfrac{1}{2}} - x^{\dfrac{1}{2}} \cdot x^{\dfrac{3}{2}} + x^{\dfrac{1}{2}} \cdot x^{\dfrac{1}{2}}} \\[12ex] \dfrac{x^{\dfrac{4}{2}} - x^{\dfrac{3}{2} - \dfrac{1}{2}} + x^1 - x^{\dfrac{1}{2} - \dfrac{1}{2}}}{x^{\dfrac{3}{2} + \dfrac{3}{2}} - x^{\dfrac{3}{2} + \dfrac{1}{2}} - x^{\dfrac{1}{2} + \dfrac{3}{2}} + x^{\dfrac{1}{2} + \dfrac{1}{2}}} \\[12ex] \dfrac{x^2 - x^{\dfrac{2}{2}} + x - x^0}{x^{\dfrac{6}{2}} - x^{\dfrac{4}{2}} - x^{\dfrac{4}{2}} + x^1} \\[12ex] \dfrac{x^2 - x + x - 1}{x^3 - x^2 - x^2 + x} \\[7ex] \dfrac{x^2 - 1}{x^3 - 2x^2 + x} \\[7ex] \dfrac{x^2 - 1^2...Difference\;\;of\;\;Two\;\;Squares}{x(x^2 - 2x + 1)...Factoring\;\;Quadratic\;\;Trinomial} \\[7ex] \dfrac{(x + 1)(x - 1)}{x(x - 1)(x - 1)} \\[5ex] \dfrac{x + 1}{x(x - 1)} $

(15.) (a.) (i.) Find m if $\log_2{(3m + 1)} = 4$

(ii.) Solve the following equation: $3\log_x{(64)} = 6$

(b.) Find an expression for p in terms of x if $\dfrac{5^{7x + 6}}{25^{-x}} = 125^p$

(c.) Find the value of $6 + \log_{b}\left(\dfrac{1}{b^3}\right) + \log_{b}\left(\sqrt{b}\right)$

(d.) Using an algebraic method, solve $4^x - \dfrac{10}{4^x} = 3$

$ (a.)(i.) \\[3ex] \log_2{(3m + 1)} = 4 \\[4ex] 3m + 1 = 2^4 ...Exponent-Logarithm\;\;Relationship \\[4ex] 3m + 1 = 16 \\[3ex] 3m = 16 - 1 \\[3ex] 3m = 15 \\[3ex] m = \dfrac{15}{3} \\[5ex] m = 5 \\[3ex] $ Check

$m = 5$
LHS	RHS
$ \log_2{(3m + 1)} \\[4ex] \log_2{3(5) + 1} \\[4ex] \log_2{15 + 1} \\[4ex] \log_2{16} \\[4ex] \log_2{2^4} \\[4ex] 4\log_2{2} ...Law\;5...Log \\[3ex] 4(1) ...Law\;4...Log \\[3ex] 4 $	4

$ (ii.) \\[3ex] 3\log_x{(64)} = 6 \\[4ex] \log_x{(64)^3} = 6 ...Law\;5...Log \\[4ex] x^6 = 64^3 ...Exponent-Logarithm\;\;Relationship \\[4ex] x = \sqrt[6]{64^3} \\[4ex] x = \left(64^3\right)^{\dfrac{1}{6}} ...Law\;7...Exp \\[5ex] x = 64^{\dfrac{1}{2}} \\[5ex] x = \sqrt{64} \\[3ex] x = 8 \\[3ex] $ Check

$x = 8$
LHS	RHS
$ 3\log_x{(64)} \\[4ex] 3\log_8{(64)} \\[4ex] 3 \cdot \log_8{8^2} \\[5ex] 3 \cdot 2\log_8{8} ...Law\;5...Log \\[4ex] 3 \cdot 2 \cdot 1 ...Law\;4...Log \\[4ex] 6 $	6

$ (b.) \\[3ex] \dfrac{5^{7x + 6}}{25^{-x}} = 125^p \\[7ex] \dfrac{5^{7x + 6}}{\left(5^2\right)^{-x}} = \left(5^3\right)^p \\[7ex] \dfrac{5^{7x + 6}}{5^{-2x}} = 5^{3p} ...Law\;5...Exp \\[7ex] 5^{(7x + 6 - (-2x))} = 5^{3p} ...Law\;2...Exp \\[5ex] 5^{7x + 6 + 2x} = 5^{3p} \\[5ex] 5^{9x + 6} = 5^{3p} \\[5ex] Same\;\;Base; \;\;Equate\;\;Exponents \\[3ex] 9x + 6 = 3p \\[3ex] 3p = 9x + 6 \\[3ex] p = \dfrac{9x + 6}{3} \\[5ex] p = \dfrac{3(3x + 2)}{3} \\[5ex] p = 3x + 2 \\[3ex] $ Check

$p = 3x + 2$
LHS	RHS
$ \dfrac{5^{7x + 6}}{25^{-x}} \\[7ex] \dfrac{5^{7x + 6}}{\left(5^2\right)^{-x}} \\[7ex] \dfrac{5^{7x + 6}}{5^{-2x}} ...Law\;5..Exp \\[7ex] 5^{(7x + 6 - (-2x))} ...Law\;2...Exp \\[5ex] 5^{7x + 6 + 2x} \\[5ex] 5^{9x + 6} $	$ 125^p \\[4ex] 125^{3x + 2} \\[4ex] \left(5^3\right)^{3x + 2} \\[4ex] 5^{9x + 6} ...Law\;5...Log $

$ (c.) \\[3ex] 6 + \log_{b}\left(\dfrac{1}{b^3}\right) + \log_{b}\left(\sqrt{b}\right) \\[7ex] 6 + \log_b{b^{-3}} + \log_b{b^{\dfrac{1}{2}}} ...Laws\;\;6\;\;and\;\;7...Exp \\[7ex] 6 + -3\log_b{b} + \dfrac{1}{2}\log_b{b} ...Law\;5...Log \\[6ex] 6 - 3(1) + \dfrac{1}{2}(1) ...Law\;4...Log \\[5ex] 6 - 3 + \dfrac{1}{2} \\[5ex] \dfrac{12}{2} - \dfrac{6}{2} + \dfrac{1}{2} \\[5ex] \dfrac{7}{2} \\[5ex] (d.) \\[3ex] 4^x - \dfrac{10}{4^x} = 3 \\[6ex] Let\;\;p = 4^x \\[4ex] p - \dfrac{10}{p} = 3 \\[5ex] LCD = p \\[3ex] p\left(p - \dfrac{10}{p}\right) = p(3) \\[5ex] p^2 - 10 = 3p \\[3ex] p^2 - 3p - 10 = 0 \\[3ex] (p + 2)(p - 5) = 0 \\[3ex] p + 2 = 0 \;\;\;OR\;\;\; p - 5 = 0 \\[3ex] p = -2 \;\;\;OR\;\;\; p = 5 \\[3ex] \implies \\[3ex] If\;\;p = -2 \\[3ex] 4^x = p \\[4ex] \log 4^x = \log(-2) \\[3ex] $ This is not possible because the logarithm of a negative number does not exist.

$ If\;\;p = 5 \\[3ex] 4^x = 5 \\[4ex] \log 4^x = \log 5 \\[4ex] x\log 4 = \log 5 \\[3ex] x = \dfrac{\log 5}{\log 4} \\[5ex] x = \log_4{5} ...Law\;6...Log \\[4ex] $ Check

$x = \log_4{5}$
LHS	RHS
$ 4^x - \dfrac{10}{4^x} \\[6ex] 4^{\log_4{5}} - \dfrac{10}{4^{\log_4{5}}} \\[7ex] 5 - \dfrac{10}{5} ...Law\;7...Log \\[5ex] 5 - 2 \\[3ex] 3 $	3

(b.) is not checked with the calculator because the answer is a variable.

For the (c.) part, we can assume any positive number for the base. We shall use the number, 7; however, you can check with any other positive number.

Number 15-1st