Further Mathematics/Mathematics (Elective) Objective Tests

Welcome to Our Site

I greet you this day,
These are the solutions to the Further Mathematics (Elective Mathematics) multiple-choice questions on the Objective Tests.
The TI-84 Plus CE shall be used for applicable questions.
Formulas, rules/laws, and theorems are not stated here. However, they are stated on the website for each topic as applicable. Please review them there.
The link to the video solutions will be provided for you. Please subscribe to the YouTube channel to be notified of upcoming livestreams. You are welcome to ask questions during the video livestreams.
If you find these resources valuable and if any of these resources were helpful in your passing the Further Mathematics tests/exams, please consider making a donation:

Cash App: $ExamsSuccess or
cash.app/ExamsSuccess

PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess

Google charges me for the hosting of this website and my other educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well. As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.

Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.

(1.) A binary operation * is defined on the set R of real numbers by $p * q = (p + q)^2 + 2p$, where p, q ∈ R.
Find the value of $(-3 * 7) + 5$

$ A.\;\; 27 \\[3ex] B.\;\; 15 \\[3ex] C.\;\; -15 \\[3ex] D.\;\; -27 \\[3ex] $

$ p * q = (p + q)^2 + 2p \\[3ex] (-3 * 7) + 5 \\[3ex] = (-3 + 7)^2 + 2(-3) + 5 \\[3ex] = 4^2 - 6 + 5 \\[3ex] = 16 - 6 + 5 \\[3ex] = 15 $

(2.) Given that $(3x - 1), (x + 1)$ and $(x - 1)$ are the first 3 consecutive terms of an exponential sequence (G.P) where x > 0.
Find the value of x.

$ A.\;\; 6 \\[3ex] B.\;\; 3 \\[3ex] C.\;\; 2 \\[3ex] D.\;\; 1 \\[3ex] $

$ (3x - 1), (x + 1), (x - 1) \\[3ex] \text{common ratio, } r = \dfrac{x + 1}{3x - 1} = \dfrac{x - 1}{x + 1} \\[5ex] (3x - 1)(x - 1) = (x + 1)(x + 1) \\[3ex] 3x^2 - 3x - x + 1 = x^2 + x + x + 1 \\[3ex] 3x^2 - 4x + 1 = x^2 + 2x + 1 \\[3ex] 3x^2 - x^2 - 4x - 2x + 1 - 1 = 0 \\[3ex] 2x^2 - 6x = 0 \\[3ex] 2x(x - 3) = 0 \\[3ex] 2x = 0 \hspace{1em}OR\hspace{1em} x - 3 = 0 \\[3ex] x = \dfrac{0}{2} \hspace{1em}OR\hspace{1em} x = 3 \\[5ex] x = 0, 3 \\[3ex] But\;\; x \gt 0 \\[3ex] Hence\;\; x = 3 $

(3.) Solve $\left(3^{x^2}\right) = \dfrac{1}{81}\left(3^{5x}\right)$

$ A.\;\; 1 \hspace{1em}or\hspace{1em} 4 \\[3ex] B.\;\; 1 \hspace{1em}or\hspace{1em} -4 \\[3ex] C.\;\; -1 \hspace{1em}or\hspace{1em} 4 \\[3ex] D.\;\; -1 \hspace{1em}or\hspace{1em} -4 \\[3ex] $

$ \left(3^{x^2}\right) = \dfrac{1}{81}\left(3^{5x}\right) \\[6ex] 3^{x^2} = \dfrac{1}{3^4}\left(3^{5x}\right) \\[7ex] 3^{x^2} = 3^{5x - 4}...Law\;2...Exp \\[5ex] \text{same base; equate exponents} \\[3ex] x^2 = 5x - 4 \\[3ex] x^2 - 5x + 4 = 0 \\[3ex] (x - 1)(x - 4) = 0 \\[3ex] x - 1 = 0 \hspace{3em}OR\hspace{3em} x - 4 = 0 \\[3ex] x = 1 \hspace{3em}OR\hspace{3em} x = 4 \\[3ex] $ Check

$x = 1, 4$
LHS	RHS
$ 3^{x^2} \\[4ex] x = 1 \\[3ex] 3^{1^2} \\[4ex] 3^1 $ $ 3^{x^2} \\[4ex] x = 4 \\[3ex] 3^{4^2} \\[4ex] 3^{16} $	$ \dfrac{1}{81}\left(3^{5x}\right) \\[6ex] x = 1 \\[3ex] \dfrac{1}{3^4}\left(3^{5(1)}\right)...Law\;5...Exp \\[7ex] \dfrac{3^5}{3^4} \\[7ex] 3^{5 - 4} ...Law\;2...Exp \\[5ex] 3^1 $ $ \dfrac{1}{81}\left(3^{5x}\right) \\[6ex] x = 4 \\[3ex] \dfrac{1}{3^4}\left(3^{5(4)}\right)...Law\;5...Exp \\[7ex] \dfrac{3^{20}}{3^4} \\[7ex] 3^{20 - 4} ...Law\;2...Exp \\[5ex] 3^{16} $

(4.) Find the equation of the axis of symmetry of $y = -4x^2 + 9x - 13$.

$ A.\;\; x = \dfrac{9}{8} \\[5ex] B.\;\; x = \dfrac{8}{9} \\[5ex] C.\;\; x = -\dfrac{8}{9} \\[5ex] D.\;\; x = -\dfrac{9}{8} \\[5ex] $

The equation of the axis of symmetry of a quadratic function is the x-coordinate of the vertex

$ y = -4x^2 + 9x - 13 \\[3ex] Compare\;\;to: y = ax^2 + bx + c \\[3ex] a = -4 \\[3ex] b = 9 \\[3ex] x-coordinate \;\;of\;\;the\;\;vertex \\[3ex] = -\dfrac{b}{2a} \\[5ex] = -\dfrac{9}{2(-4)} \\[5ex] = \dfrac{9}{8} \\[3ex] $ This is the axis of symmetry of the quadratic function.

(5.) If $x = \dfrac{p\sqrt{q}}{r}$, which of the following represents $\log_{10}x$?

$ A.\;\; \dfrac{\log_{10}p \times \log_{10}\sqrt{q}}{\log_{10}r} \\[6ex] B.\;\; \log_{10} p + \dfrac{1}{2}\log_{10}q + \log_{10}r \\[5ex] C.\;\; \dfrac{\log_{10} p + \dfrac{1}{2}\log_{10} q}{\log_{10} r} \\[7ex] D.\;\; \log_{10} p + \dfrac{1}{2}\log_{10} q - \log_{10} r \\[5ex] $

$ \log_{10} x = \log x \\[3ex] x = \dfrac{p\sqrt{q}}{r} \\[3ex] \text{Introduce log to both sides} \\[3ex] \log x = \log\left(\dfrac{p\sqrt{q}}{r}\right) \\[5ex] = \log p + \log \sqrt{q} - \log r ...Laws\;1\;\;and\;\;2...Log \\[4ex] = \log p + \log q^{\dfrac{1}{2}} - \log r ...Law\;7...Exp \\[5ex] = \log p + \dfrac{1}{2}\log q - \log r ...Law\;5...Log \\[5ex] = \log_{10} p + \dfrac{1}{2}\log_{10}q + \log_{10}r $

(6.) Given that $f(x) = \dfrac{5x + 8}{7 - 3x},\;\;x \ne \dfrac{7}{3}$, find $f^{-1}(2)$

$ A.\;\; \dfrac{11}{6} \\[5ex] B.\;\; \dfrac{6}{11} \\[5ex] C.\;\; -\dfrac{6}{11} \\[5ex] D.\;\; -\dfrac{11}{6} \\[5ex] $

$ f(x) = \dfrac{5x + 8}{7 - 3x},\;\;x \ne \dfrac{7}{3} \\[5ex] y = \dfrac{5x + 8}{7 - 3x} \\[5ex] \text{Interchange x and y} \\[3ex] x = \dfrac{5y + 8}{7 - 3y} \\[5ex] \text{Solve for y} \\[3ex] 5y + 8 = x(7 - 3y) \\[3ex] 5y + 8 = 7x - 3xy \\[3ex] 5y + 3xy = 7x - 8 \\[3ex] y(5 + 3x) = 7x - 8 \\[3ex] y = \dfrac{7x - 8}{5 + 3x} \\[5ex] \text{This value of y is the inverse function} \\[3ex] y^{-1} = \dfrac{7x - 8}{5 + 3x} \\[5ex] f^(-1)(x) = \dfrac{7x - 8}{3x + 5} \\[5ex] f^(-1)(2) = \dfrac{7(2) - 8}{3(2) + 5} \\[5ex] = \dfrac{14 - 8}{6 + 5} \\[5ex] = \dfrac{6}{11} $

(7.) If $\displaystyle\int_4^9 \left(\dfrac{1}{\sqrt{x}}\right) dx = y$, find the value of y

$ A.\;\; \dfrac{1}{6} \\[5ex] B.\;\; \dfrac{2}{3} \\[5ex] C.\;\; 2 \\[3ex] D.\;\; 3 \\[3ex] $

$ \dfrac{1}{\sqrt{x}} \\[3ex] = \dfrac{1}{x^{\dfrac{1}{2}}}...Law\;7...Exp \\[7ex] = x^{-\dfrac{1}{2}} ...Law\;6...Exp \\[5ex] \implies \\[3ex] \displaystyle\int \dfrac{1}{\sqrt{x}} dx \\[5ex] = \displaystyle\int x^{-\dfrac{1}{2}} dx \\[5ex] = \dfrac{x^{-\dfrac{1}{2} + 1}}{-\dfrac{1}{2} + 1}...Power\;\;Rule \\[7ex] = \dfrac{x^{\dfrac{1}{2}}}{\dfrac{1}{2}} \\[7ex] = x^{\dfrac{1}{2}} \div \dfrac{1}{2} \\[5ex] = \sqrt{x} * \dfrac{2}{1} \\[5ex] = 2\sqrt{x} \\[5ex] \implies \\[3ex] \displaystyle\int_4^9 \left(\dfrac{1}{\sqrt{x}}\right) dx \\[7ex] = \left[2\sqrt{x}\right]_4^9 \\[5ex] = 2\sqrt{9} - 2\sqrt{4} \\[3ex] = 2(\sqrt{9} - \sqrt{4}) \\[3ex] = 2(3 - 2) \\[3ex] = 2(1) \\[3ex] = 2 \\[3ex] y = 2 $

(8.) Find the sum to infinity of $5 + \dfrac{10}{3} + \dfrac{20}{9} + $

$ A.\;\; \dfrac{5}{3} \\[5ex] B.\;\; 3 \\[3ex] C.\;\; 5 \\[3ex] D.\;\; 15 \\[3ex] $

$ 5 + \dfrac{10}{3} + \dfrac{20}{9} + \\[5ex] \text{first term, } a = 5 \\[3ex] \text{common ratio, } r = \dfrac{10}{3} \div 5 \\[5ex] r = \dfrac{10}{3} * \dfrac{1}{5} \\[5ex] r = \dfrac{2}{3} \\[5ex] \text{Sum to infinity, } S_\infty = \dfrac{a}{1 - r} \\[5ex] = a \div (1 - r) \\[3ex] = 5 \div \left(1 - \dfrac{2}{3}\right) \\[5ex] = 5 \div \dfrac{1}{3} \\[5ex] = 5 * 3 \\[3ex] = 15 $

(9.) Given that $^{(n + 1)}P_2 = 12$, find the value of n.

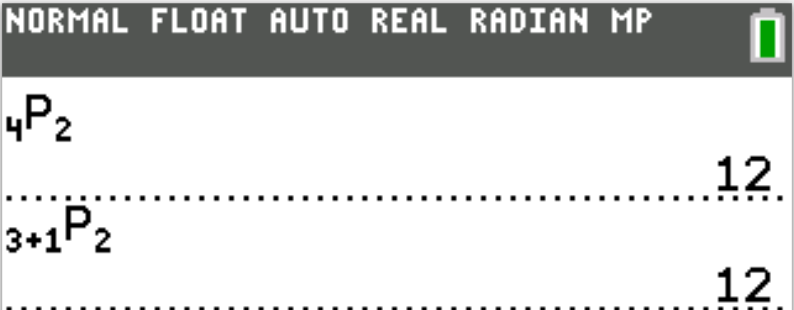
$ A.\;\; 12 \\[3ex] B.\;\; 6 \\[3ex] C.\;\; 4 \\[3ex] D.\;\; 3 \\[3ex] $

$ ^nP_r = \dfrac{n!}{(n - r)!} \\[5ex] ^{(n + 1)}P_2 = 12 \\[5ex] \dfrac{(n + 1)!}{(n + 1 - 2)!} = 12 \\[5ex] \dfrac{(n + 1) \cdot n \cdot (n - 1)!}{(n - 1)!} = 2 \\[5ex] n^2 + n = 12 \\[3ex] n^2 + n - 12 = 0 \\[3ex] (n + 4)(n - 3) = 0 \\[3ex] n + 4 = 0 \hspace{1em}OR\hspace{1em} n - 3 = 0 \\[3ex] n = -4 \hspace{1em}OR\hspace{1em} n = 3 \\[3ex] n \;\; \text{cannot be negative because it has to be countable} \\[3ex] \therefore n = 3 $

(11.) If $\begin{bmatrix} 4 & -2 \\[2ex] x & 6 \end{bmatrix}\begin{bmatrix} 2 \\[2ex] -5 \end{bmatrix} = 4\begin{bmatrix} 4.5 \\[2ex] -11 \end{bmatrix}$, find the value of x.

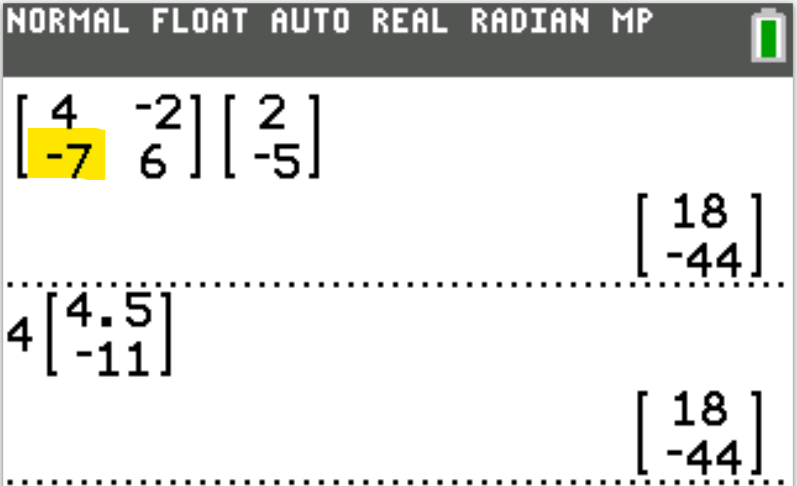
$ A.\;\; -9 \\[3ex] B.\;\; -7 \\[3ex] C.\;\; 7 \\[3ex] D.\;\; 9 \\[3ex] $

$ \begin{bmatrix} 4 & -2 \\[2ex] x & 6 \end{bmatrix}\begin{bmatrix} 2 \\[2ex] -5 \end{bmatrix} = 4\begin{bmatrix} 4.5 \\[2ex] -11 \end{bmatrix} $

$ \begin{bmatrix} 4(2) + (-2)(-5) \\[2ex] x(2) + 6(-5) \end{bmatrix} = \begin{bmatrix} 4(4.5) \\[2ex] 4(-11) \end{bmatrix} $

$ \begin{bmatrix} 8 + 10 \\[2ex] 2x - 30 \end{bmatrix} = \begin{bmatrix} 18 \\[2ex] -44 \end{bmatrix} $

$ 2x - 30 = -44 \\[3ex] 2x = -44 + 30 \\[3ex] 2x = -14 \\[3ex] x = -\dfrac{14}{2} \\[5ex] x = -7 $

(12.) If the curve $y = 3x^2 + 10x + 2$ passes through (x, −6), find the least value of x.

$ A.\;\; -5 \\[3ex] B.\;\; -4 \\[3ex] C.\;\; -3 \\[3ex] D.\;\; -2 \\[3ex] $

The curve $y = 3x^2 + 10x + 2$ passes through (x, −6)
We do not know the value of x (we need to find it)
But we do know the value of y = −6

$ y = 3x^2 + 10x + 2 \\[3ex] -6 = 3x^2 + 10x + 2 \\[3ex] 3x^2 + 10x + 2 = -6 \\[3ex] 3x^2 + 10x + 2 + 6 = 0 \\[3ex] 3x^2 + 10x + 8 = 0 \\[3ex] 3x^2 + 6x + 4x + 8 = 0 \\[3ex] 3x(x + 2) + 4(x + 2) = 0 \\[3ex] (x + 2)(3x + 4) = 0 \\[3ex] x + 2 = 0 \hspace{1em}OR\hspace{1em} 3x + 4 = 0 \\[3ex] x = -2 \hspace{1em}OR\hspace{1em} 3x = -4 \\[3ex] x = -2 \hspace{1em}OR\hspace{1em} x = -\dfrac{4}{3} \\[5ex] -2 \lt -\dfrac{4}{3} \\[5ex] $ ∴ the least value of x = −2

(13.) For what values of x is $11x + 12 \gt x^2$

$ A.\;\; -1 \lt x \lt 12 \\[3ex] B.\;\; -1 \lt x \lt \dfrac{1}{12} \\[5ex] C.\;\; x \le -1 \;\;or\;\; x \ge \dfrac{1}{12} \\[5ex] D.\;\; x \le -1 \;\;or\;\; x \ge 12 \\[3ex] $

$ 11x + 12 \gt x^2 \\[3ex] x^2 \lt 11x + 12 \\[3ex] x^2 - 11x - 12 \lt 0 \\[3ex] (x + 1)(x - 12) \lt 0 \\[3ex] Assume:\;\;(x + 1)(x - 12) = 0 \\[3ex] x + 1 = 0 \;\;\;OR\;\;\; x - 12 = 0 \\[3ex] x = -1 \;\;\;OR\;\;\; x = 12 \\[3ex] Test\;\;Intervals\;\;are: \\[3ex] x \lt -1 \\[3ex] -1 \lt x \lt 12 \\[3ex] x \gt 12 \\[3ex] $

Test Intervals: Let:	x < −1 x = −2	−1 < x < 12 x = 0	x > 12 x = 13
$x + 1$	−	+	+
$x - 12$	−	−	+
$(x + 1)(x - 12)$	+	−	+

The second test interval gives the solution of the inequality because a negative number is less than 0
Set Notation: {x | −1 < x < 12}
Interval Notation: (−1, 12)

Check

(−1, 12)
Let x = 0
LHS	RHS
$ 11x + 12 \\[3ex] 11(0) + 12 \\[3ex] 0 + 12 \\[3ex] 12 $	$ x^2 \\[3ex] 0^2 \\[3ex] 0 $
12 > 0

(14.) The table shows the distribution of marks obtained by students in a Mathematics test.

Marks	1 — 5	6 — 10	11 — 15	16 — 20
Number of Students	5	5	x	8
Cumulative Frequency	5	10	12	y

Find the value of $(2x + y)$

$ A.\;\; 38 \\[3ex] B.\;\; 34 \\[3ex] C.\;\; 28 \\[3ex] D.\;\; 24 \\[3ex] $

Based on the Cumulative Frequency:

$ 5 \\[3ex] 5 + 5 = 10 \\[3ex] 10 + x = 12 \implies x = 12 - 10 = 2 \\[3ex] 12 + 8 = y \implies y = 20 \\[5ex] 2x + y \\[3ex] = 2(2) + 20 \\[3ex] = 4 + 20 \\[3ex] = 24 $

(15.) If $\cos(y) = -\dfrac{1}{3}$, where $90^\circ \lt y \lt 180^\circ$, find cosec(y)

$ A.\;\; \dfrac{3}{4}\sqrt{2} \\[5ex] B.\;\; \dfrac{4}{3}\sqrt{2} \\[5ex] C.\;\; -\dfrac{3}{4}\sqrt{2} \\[5ex] D.\;\; -\dfrac{4}{3}\sqrt{2} \\[5ex] $

$ \sin^2 y + \cos^2 y = 1 ...\text{Pythagorean Identity} \\[3ex] \sin^2 y = 1 - \cos^2 y \\[3ex] = 1 - \left(-\dfrac{1}{3}\right)^2 \\[5ex] = 1 - \dfrac{1}{9} \\[5ex] = \dfrac{8}{9} \\[5ex] \sin y = \pm \sqrt{\dfrac{8}{9}} \\[5ex] \text{But } 90^\circ \lt y \lt 180^\circ \;\;\text{is in the 2nd Quadrant} \\[3ex] \text{In the 2nd Quadrant, sine is positive} \\[3ex] \implies \\[3ex] \sin y = \sqrt{\dfrac{8}{9}} \\[5ex] = \dfrac{\sqrt{4 * 2}}{3} \\[5ex] = \dfrac{2\sqrt{2}}{3} \\[5ex] \csc y = \dfrac{1}{\sin y} ...\text{Reciprocal Identity} \\[5ex] \csc y = 1 \div \sin y \\[3ex] = 1 \div \dfrac{2\sqrt{2}}{3} \\[5ex] = 1 * \dfrac{3}{2\sqrt{2}} \\[5ex] = \dfrac{3}{2\sqrt{2}} * \dfrac{\sqrt{2}}{\sqrt{2}} \\[5ex] = \dfrac{3\sqrt{2}}{2 * 2} \\[5ex] = \dfrac{3\sqrt{2}}{4} $

(16.) A ball is thrown vertically upwards with a velocity of 12$ms^{-1}$.
Calculate the maximum height reached.
[Take g = 10$ms^{-2}$]

$ A.\;\; 10.0 m \\[3ex] B.\;\; 9.6 m \\[3ex] C.\;\; 7.2 m \\[3ex] D.\;\; 6.4 m \\[3ex] $

We shall use one of the equations of motion:

$ v^2 = u^2 + 2as \\[3ex] $ When the ball is thrown vertically upwards:
(1.) The final velocity, v is zero.
But we have an initial velocity, u = 12$ms^{-1}$

(2.) The acceleration, a is negative because it is working against gravity
Hence, it is the negative value of the acceleration due to gravity
a = −g

(3.) We shall take the distance, s to be the maximum height, H
So, we have

$ v^2 = u^2 + 2as \\[3ex] becomes \\[3ex] v^2 = u^2 - 2gH \\[3ex] 0^2 = 12^2 - 2(10) * H \\[3ex] 0 = 144 - 20H \\[3ex] 20H = 144 \\[3ex] H = \dfrac{144}{20} \\[5ex] H = 7.2\;m $

(17.) Find the equation of a circle with centre (6, −11) and radius 8 units.

$ A.\;\; x^2 + y^2 - 12x + 22y + 93 = 0 \\[3ex] B.\;\; x^2 + y^2 - 12x - 22y + 93 = 0 \\[3ex] C.\;\; x^2 + y^2 - 12x + 22y - 93 = 0 \\[3ex] D.\;\; x^2 + y^2 - 12x - 22y - 93 = 0 \\[3ex] $

The equation of a circle in the (x, y) coordinate plane with center (h, k) and radius, r is:

$ (x - h)^2 + (y - k)^2 = r^2 \\[3ex] Center:\;\; (h, k) = (6, -11) \\[3ex] h = 6 \\[3ex] k = -11 \\[3ex] r = 8 \\[3ex] \implies \\[3ex] (x - 6)^2 + (y - -11)^2 = 8^2 \\[3ex] (x - 6)^2 + (y + 11)^2 = 64 \\[3ex] [(x - 6)(x - 6)] + [(y + 11)(y + 11)] - 64 = 0 \\[3ex] (x^2 - 6x - 6x + 36) + (y^2 + 11y + 11y + 121) - 64 = 0 \\[3ex] x^2 - 12x + 36 + y^2 + 22y + 121 - 64 = 0 \\[3ex] x^2 + y^2 - 12x + 22y + 93 = 0 $

(19.) A committee of two is to be selected from 5 boys and 3 girls.
What is the probability that it will consist of a boy and a girl?

$ A.\;\; \dfrac{15}{28} \\[5ex] B.\;\; \dfrac{5}{28} \\[5ex] C.\;\; \dfrac{3}{28} \\[5ex] D.\;\; \dfrac{2}{7} \\[5ex] $

total number = 5 boys and 3 girls = 8 people
selected number = 1 boy and 1 girl = 2 people

Let:
S = sample space
$n(S) = C(8, 2)$

A = event of selecting 1 boy from 5 boys
$n(A) = C(5, 1)$

B = event of selecting 1 girl from 3 girls
$n(B) = C(3, 1)$

$ C(n, r) = \dfrac{n!}{(n - r) r!} \\[5ex] n(S) = C(8, 2) = \dfrac{8!}{(8 - 2)! * 2!} \\[5ex] = \dfrac{8 * 7 * 6!}{6! * 2 * 1} \\[5ex] = 4 * 7 \\[3ex] = 28 \\[5ex] n(A) = C(5, 1) = \dfrac{5!}{(5 - 1)! * 1!} \\[5ex] = \dfrac{5 * 4!}{4! * 1} \\[5ex] = 5 \\[5ex] n(B) = C(3, 1) = \dfrac{3!}{(3 - 1)! * 1!} \\[5ex] = \dfrac{3 * 2!}{2! * 1} \\[5ex] = 3 \\[5ex] $ Probability of selecting 1 boy from 5 boys AND 1 girl from 3 girls is:

$ = \dfrac{n(A) * n(B)}{n(S)} \\[5ex] = \dfrac{5 * 3}{28} \\[5ex] = \dfrac{15}{28} $

(20.) Two bodies having masses of 6 kg and 4 kg moving in the same direction with velocities 2 $ms^{-1}$ and 4 $ms^{-1}$ respectively, collide with each other.
If they stick together after collision, find their common velocity.

$ A.\;\; 1.6ms^{-1} \\[3ex] B.\;\; 2.8ms^{-1} \\[3ex] C.\;\; 3.2ms^{-1} \\[3ex] D.\;\; 3.6ms^{-1} \\[3ex] $

Let the:
First body be P: mass of 6 kg and velocity of 2 m/s
Second body be Q: mass of 4 kg and velocity of 4 m/s
Momentum = mass × velocity

$ \underline{\text{Before Collision}} \\[3ex] \text{Momentum of Body P} = 6 \times 2 = 12\;kgm/s \\[3ex] \text{Momentum of Body Q} = 4 \times 4 = 16\;kgm/s \\[3ex] \text{Total Momentum} = 12 + 16 = 28\;kgm/s \\[5ex] \underline{\text{After Collision}} \\[3ex] \text{Mass of P and Q after they stick together} = 6 + 4 = 10\;kg \\[3ex] \text{Let the common velocity} = v\;m/s \\[3ex] \text{Total Momentum} = 10 \times v = 10v\;kgm/s \\[5ex] \text{Based on the Principle of Conservation of Momentum:} \\[3ex] 28 = 10v \\[3ex] 10v = 28 \\[3ex] v = \dfrac{28}{10} \\[5ex] v = 2.8\;kgms^{-1} $

Top