General Mathematics/Mathematics (Core) Objective Tests
Welcome to Our Site
I greet you this day,
These are the solutions to the General Mathematics (Core Mathematics) multiple-choice questions on the
Objective Tests.
The TI-84 Plus CE shall be used for applicable questions.
Formulas, rules/laws, and theorems are not stated here. However, they are stated on the website for each topic
as applicable. Please review them there.
The link to the video solutions will be provided for you. Please subscribe to the YouTube channel to be notified
of upcoming livestreams.
You are welcome to ask questions during the video livestreams.
If you find these resources valuable and if any of these resources were helpful in your passing the
Mathematics tests/exams, please consider making a donation:
Cash App: $ExamsSuccess or
cash.app/ExamsSuccess
PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess
Google charges me for the hosting of this website and my other
educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well.
As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.
Comments, ideas, areas of improvement, questions, and constructive
criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.
Calculate, correct to the nearest degree, the angle of depression of the point from the top of the wall.
$ A.\;\; 25^\circ \\[3ex] B.\;\; 23^\circ \\[3ex] C.\;\; 67^\circ \\[3ex] D.\;\; 65^\circ \\[3ex] $
Let us represent the information diagrammatically.
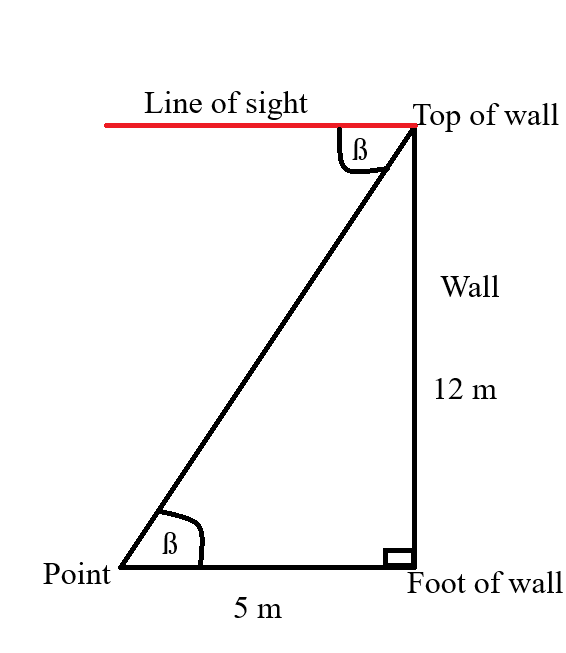
$ \beta = \text{angle of depression} \\[3ex] \beta = \beta ...\text{alternate interior angles are congruent} \\[5ex] \underline{\text{SOHCAHTOA}} \\[3ex] \tan\beta = \dfrac{opp}{adj} = \dfrac{12}{5} \\[5ex] \beta = \tan{-1}\left(\dfrac{12}{5}\right) \\[5ex] \beta = 67.38013505 \\[3ex] \beta \approx 67^\circ ...\text{to the nearest degree} $
Find the value of x.
$ A.\;\; 3 \\[3ex] B.\;\; 8 \\[3ex] C.\;\; 6 \\[3ex] D.\;\; 5 \\[3ex] $
$ Point\;1(3, 6) \hspace{3em} Point\;2(x, 4) \\[3ex] x_1 = 3 \hspace{6em} x_2 = x \\[3ex] y_1 = 6 \hspace{6em} y_2 = 4 \\[3ex] Gradient = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] -\dfrac{2}{5} = \dfrac{4 - 6}{x - 3} \\[5ex] \text{Cross Multiply} \\[3ex] -2(x - 3) = (4 - 6)(5) \\[3ex] -2(x - 3) = (-2)(5) \\[3ex] \text{Divide both sides by } -2 \\[3ex] x - 3 = 5 \\[3ex] x = 5 + 3 \\[3ex] x = 8 $
Calculate, correct to the nearest cm, the depth of the kerosene in the container.
$\left[Take\;\;\pi = \dfrac{22}{7}\right]$
$ A.\;\; 240\;cm \\[3ex] B.\;\; 552\;cm \\[3ex] C.\;\; 480\;cm \\[3ex] D.\;\; 595\;cm \\[3ex] $
The kerosene is poured into a cylindrical container
So, we shall be looking at the volume of a cylinder
V = π r²h
where:
V = volume of the cylinder = volume of the kerosene = 85 liters = 85 dm³
r = radius of the cylinder = 7 cm
h = height of the cylinder = depth of the kerosene = ?
We need to convert 85 dm³ to cm³ before we can calculate the depth of the kerosene
$ \underline{\text{Unity Fraction Method}} \\[3ex] 85\;dm^3 \;\;to\;\; cm^3 \\[3ex] = 85\;dm * dm * dm * \dfrac{...m}{...dm} * \dfrac{...m}{...dm} * \dfrac{...m}{...dm} * \dfrac{...cm}{...m} * \dfrac{...cm}{...m} * \dfrac{...cm}{...m} \\[5ex] = 85\;dm * dm * dm * \dfrac{10^{-1}\;m}{1\;dm} * \dfrac{10^{-1}\;m}{1\;dm} * \dfrac{10^{-1}\;m}{1\;dm} * \dfrac{1\;cm}{10^{-2}\;m} * \dfrac{1\;cm}{10^{-2}\;m} * \dfrac{1\;cm}{10^{-2}\;m}...Table\;1 \\[5ex] = \dfrac{85 * 10^{-1 - 1 - 1}}{10^{-2 - 2 - 2}} ...Law\;1...Exp \\[5ex] = \dfrac{85 * 10^{-3}}{10^{-6}} \\[5ex] = 85 * 10^{-3 - (-6)} ...Law\;2...Exp \\[3ex] = 85 * 10^{-3 + 6} \\[3ex] = 85 * 10^3 \\[3ex] = 85 * 1000 \\[3ex] = 85000\;cm^3 \\[5ex] V = \pi r^2 h \\[3ex] h = \dfrac{V}{\pi r^2} \\[5ex] = V \div (\pi r^2) \\[3ex] = 85000 \div \left(\dfrac{22}{7} * 7^2\right) \\[5ex] = 85000 \div (22 * 7) \\[3ex] = 551.9480519 \\[3ex] \approx 552\;cm $
$ A.\;\; \dfrac{11}{2} \\[5ex] B.\;\; \dfrac{121}{8} \\[5ex] C.\;\; \dfrac{121}{4} \\[5ex] D.\;\; 121 \\[3ex] $
We can solve this question using at least two approches.
Use any approach you prefer.
1st Approach: Technique used in Completing the Square method.
m =
Square of
half of
the coefficient of x
$ x^2 - 11x + m \\[3ex] \text{coefficient of x} = -11 \\[3ex] \text{half of it} = \dfrac{1}{2} * -11 = -\dfrac{11}{2} \\[5ex] \text{square it} = \left(-\dfrac{11}{2}\right)^2 \\[5ex] m = \left(-\dfrac{11}{2}\right)^2 \\[5ex] m = \dfrac{121}{4} \\[3ex] $ 2nd Approach: Expression as a Perfect Square
Reviewing the expression given to us: $x^2 - 11x + m$
The negative value of the coefficient of x (−11) implies that the expression would resemble:
the kind of perfect square expressed as $(x - y)^2$
Notice the term: −y
We shall expand the perfect square expression, equate it to the expression given to us, and determine the value of m
$ (x - y)^2 \\[3ex] = (x - y)(x - y) \\[3ex] = x^2 - xy - xy + y^2 \\[3ex] = x^2 - 2xy + y^2 \\[5ex] Compare: \\[3ex] x^2 - 11x + m \hspace{2em}to\hspace{2em} x^2 - 2xy + y^2 \\[3ex] 2y = 11 \\[3ex] y = \dfrac{11}{2} \\[5ex] m = y^2 \\[3ex] m = \left(\dfrac{11}{2}\right)^2 \\[5ex] m = \dfrac{121}{4} \\[3ex] $ Student: Mr. C
Teacher: Yes, my dear Student
Student: If we were given $x^2 + 11x + m$ and asked to find $m$ and we prefer to use the 2nd Approach, I guess the perfect square expression would be $(x + y)^2$
Is that correct?
Teacher: It is correct.
As it is easier to compare and solve.
But, you can still use $(x - y)^2$ and compare and still get the same answer.
Student: So, if we used $(x + y)^2$ for the question we just did, we would get the same answer?
Teacher: Yes...
Student: Can we do it?
Teacher: Sure, let's do it.
$ (x + y)^2 \\[3ex] = (x + y)(x + y) \\[3ex] = x^2 + xy + xy + y^2 \\[3ex] = x^2 + 2xy + y^2 \\[5ex] Compare: \\[3ex] x^2 - 11x + m \hspace{2em}to\hspace{2em} x^2 + 2xy + y^2 \\[3ex] 2y = -11 \\[3ex] y = -\dfrac{11}{2} \\[5ex] m = y^2 \\[3ex] m = \left(-\dfrac{11}{2}\right)^2 \\[5ex] m = \dfrac{121}{4} $
Calculate, correct to the nearest whole number, the area of the triangle.
$ A.\;\; 13\;cm^2 \\[3ex] B.\;\; 17\;cm^2 \\[3ex] C.\;\; 21\;cm^2 \\[3ex] D.\;\; 19\;cm^2 \\[3ex] $
We can solve this question using at least two approaches.
Use any approach that you prefer.
1st Approach: Heron's Formula
Let:
a, b, c = sides of the triangle
s = semi-perimeter
$ a = 4\;cm \\[3ex] b = 9\;cm \\[3ex] c = 11\;cm \\[3ex] s = \dfrac{a + b + c}{2} \\[5ex] = \dfrac{4 + 9 + 11}{2} \\[5ex] = 12\;cm \\[5ex] s - a = 12 - 4 = 8\;cm \\[3ex] s - b = 12 - 9 = 3\;cm \\[3ex] s - c = 12 - 11 = 1\;cm \\[3ex] s(s - a)(s - b)(s - c) = 12(8)(3)(1) = 288\;cm \\[5ex] Area = \sqrt{s(s - a)(s - b)(s - c)} \\[3ex] = \sqrt{288} \\[3ex] = 16.97056275 \\[3ex] \approx 17\;cm^2 \\[3ex] $ 2nd Approach: Cosine's Law and Area of Triangle Formula
Let us represent the information diagrammatically for easier comprehension

$ a = 4\;cm \\[3ex] b = 9\;cm \\[3ex] c = 11\;cm \\[5ex] \underline{\text{Cosine Law}} \\[3ex] c^2 = a^2 + b^2 - 2ab \cos \angle C \\[3ex] 11^2 = 4^2 + 9^2 - 2(4)(9) \cos \angle C \\[3ex] 121 = 16 + 81 - 72 \cos \angle C \\[3ex] 72\cos\angle C = 16 + 81 - 121 \\[3ex] \cos\angle C = \dfrac{-24}{72} \\[5ex] \angle C = \cos^{-1}\left(-\dfrac{24}{72}\right) \\[5ex] \angle C = 109.4712206^\circ \\[5ex] \underline{\text{Area of a triangle}} \\[3ex] Area = \dfrac{1}{2} ab \sin \angle C \\[5ex] = \dfrac{1}{2} * 4 * 9 * \sin 109.4712206 \\[5ex] = 16.97056275 \\[3ex] \approx 17\;cm^2 $
12% are children, 56 are men and the rest are women.
If one person is selected at random from the hall, find the probability that a woman is selected.
$ A.\;\; \dfrac{3}{25} \\[5ex] B.\;\; \dfrac{11}{25} \\[5ex] C.\;\; \dfrac{8}{25} \\[5ex] D.\;\; \dfrac{14}{25} \\[5ex] $
$ \text{n(Sample Space)} = 175 \\[3ex] \text{n(Children)} = 12\% * 175 = 0.12(175) = 21 \\[3ex] \text{n(Men)} = 56 \\[3ex] \text{n(Women)} = 175 - (21 + 56) = 98 \\[3ex] \text{Probability(a woman)} = \dfrac{\text{n(Women)}}{\text{n(Sample Space)}} \\[5ex] = \dfrac{98}{175} \\[5ex] = \dfrac{14}{25} $
If the percentage error was 5%, what was the actual length?
$ A.\;\; 3.80\;m \\[3ex] B.\;\; 3.78\;m \\[3ex] C.\;\; 4.18\;m \\[3ex] D.\;\; 4.20\;m \\[3ex] $
$ \text{Measured Value} = 3.99\;m \\[3ex] \text{Actual Value} = p \\[3ex] \%Error = 5\% \\[5ex] \%Error = \dfrac{\text{|Actual Value – Measured Value|}}{\text{Actual Value}} * 100 \\[5ex] \dfrac{5}{100} = \dfrac{|p - 3.99|}{p} \\[5ex] 100(p - 3.99) = 5p \\[3ex] 100p - 399 = 5p \\[3ex] 100p - 5p = 399 \\[3ex] 95p = 399 \\[3ex] p = \dfrac{399}{95} \\[5ex] p = 4.2\;m $
What is the average speed of the entire journey?
$ A.\;\; 44\dfrac{4}{9}\; km/h \\[5ex] B.\;\; 45\dfrac{5}{9}\; km/h \\[5ex] C.\;\; 47\dfrac{1}{4}\; km/h \\[5ex] D.\;\; 63\dfrac{1}{4}\; km/h \\[5ex] $
To find the average speed, let us find the total distance and divide it by the total time
$ s.......t.......d \\[3ex] \text{speed × time = distance} \\[3ex] speed = \dfrac{distance}{time} \\[5ex] \underline{\text{1st part of journey}} \\[3ex] distance = 80\;km \\[3ex] time = 2\;hr \\[5ex] \underline{\text{2nd part of journey}} \\[3ex] time = 2.5\;hr \\[3ex] speed = 50\;km/h \\[3ex] distance = 50(2.5) = 125\;km \\[5ex] \underline{\text{Entire journey}} \\[3ex] \text{total distance} = 80 + 125 = 205\;km \\[3ex] \text{total time} = 2 + 2.5 = 4.5\;hr \\[3ex] \text{average speed} = \dfrac{\text{total distance}}{\text{total time}} \\[5ex] = \dfrac{125}{4.5} \\[5ex] = \dfrac{1250}{45} \\[5ex] = \dfrac{410}{9} \\[5ex] = 45\dfrac{5}{9}\; km/h $
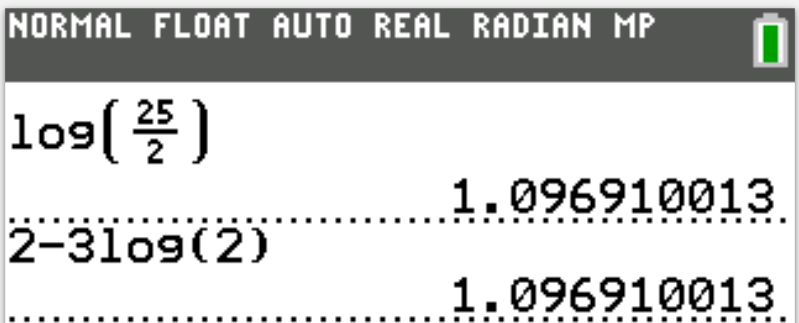
$ A.\;\; \dfrac{5}{2} \\[5ex] B.\;\; \dfrac{2}{5} \\[5ex] C.\;\; \dfrac{2}{25} \\[5ex] D.\;\; \dfrac{25}{2} \\[5ex] $
$ \log x = 2 - 3\log 2 \\[3ex] \log x = \log 10^2 - \log 2^3 ...Law\;5...Log \\[4ex] \log x = \log 100 - \log 8 \\[3ex] \log x = \log\left(\dfrac{100}{8}\right) ...Law\;2...Log \\[5ex] \text{same base; equate terms} \\[3ex] x = \dfrac{100}{8} \\[5ex] = \dfrac{25}{2} $
Find the value of k
$ A.\;\; 2 \\[3ex] B.\;\; 3 \\[3ex] C.\;\; 7 \\[3ex] D.\;\; 5 \\[3ex] $
$ y = x^2 - 5x + k \\[3ex] \text{passes through (3, 1) implies that:} \\[3ex] x = 3 \\[3ex] y = 1 \\[3ex] \implies \\[3ex] 1 = 3^2 - 5(3) + k \\[3ex] 1 = 9 - 15 + k \\[3ex] 1 = -6 + k \\[3ex] -6 + k = 1 \\[3ex] k = 1 + 6 \\[3ex] k = 7 $
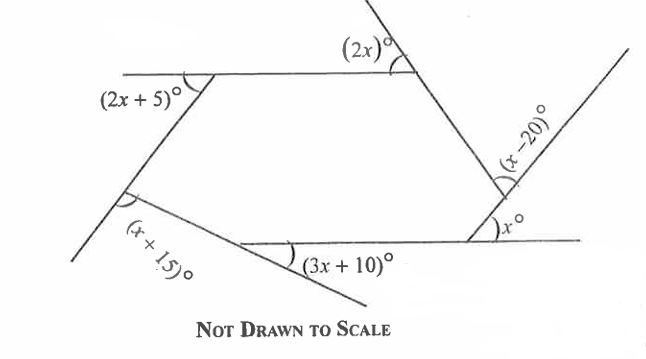
Find the value of x in the diagram.
$ A.\;\; 41 \\[3ex] B.\;\; 37 \\[3ex] C.\;\; 35 \\[3ex] D.\;\; 31 \\[3ex] $
We can solve this question using at least two approaches.
Use any approach you prefer, however, I'll go with the first approach.
1st Approach: Exterior Angle Sum Theorem: The sum of the exterior angles of a polygon (regular and irregular polygons) is 360°
This implies that:
$ (2x + 5)^\circ + (2x)^\circ + (x - 20)^\circ + x^\circ + (3x + 10)^\circ + (x + 15)^\circ = 360^\circ \\[3ex] 2x + 5 + 2x + x - 20 + x + 3x + 10 + x + 15 = 360 \\[3ex] 10x + 10 = 360 \\[3ex] 10x = 360 - 10 \\[3ex] 10x = 350 \\[3ex] x = \dfrac{350}{10} \\[5ex] x = 35^\circ \\[3ex] $ 2nd Approach: Interior Angle Sum Theorem: The sum of the interior angles of a polygon (regular and irregular polygons) is $180(n - 2)$
The hexagon (which is in question) has 6 sides.
$ \underline{\text{By Formula}} \\[3ex] \text{Sum of the interior angles of a hexagon} = 180(6 - 2) \\[3ex] = 180(4) \\[3ex] = 720^\circ \\[3ex] $ We are not given the interior angles. So, we need to find each of them.
To find each interior angle, we use the theorem that states that the sum of angles on a straight line is 180°
$ \text{The interior angles are:} \\[3ex] 180 - (2x + 5) = 180 - 2x - 5 = 175 - 2x \\[3ex] 180 - 2x \\[3ex] 180 - (x - 20) = 180 - x + 20 = 200 - x \\[3ex] 180 - x \\[3ex] 180 - (3x + 10) = 180 - 3x - 10 = 170 - 3x \\[3ex] 180 - (x + 15) = 180 - x - 15 = 165 - x \\[5ex] \text{Sum of the interior angles of the hexagon} \\[3ex] = 175 - 2x + 180 - 2x + 200 - x + 180 - x + 170 - 3x + 165 - x \\[3ex] = 1070 - 10x \\[3ex] \text{Equate the two sums} \\[3ex] 720 = 1070 - 10x \\[3ex] 10x = 1070 - 720 \\[3ex] 10x = 350 \\[3ex] x = \dfrac{350}{10} \\[5ex] x = 35^\circ. $
$ A.\;\; 1.5 \\[3ex] B.\;\; 2.5 \\[3ex] C.\;\; 2.0 \\[3ex] D.\;\; 3.0 \\[3ex] $
$ x : y : z = 2 : 3 : 4 \\[3ex] x = 2 \\[3ex] y = 3 \\[3ex] z = 4 \\[5ex] \dfrac{9x + 3y}{6z - 2y} \\[5ex] = \dfrac{9(2) + 3(3)}{6(4) - 2(3)} \\[5ex] = \dfrac{18 + 9}{24 - 6} \\[5ex] = \dfrac{27}{18} \\[5ex] = 1.5 $
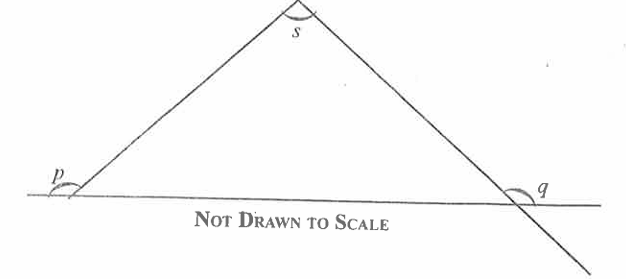
In the diagram, p + q = 250°.
Find the angle marked x
$ A.\;\; 70^\circ \\[3ex] B.\;\; 110^\circ \\[3ex] C.\;\; 290^\circ \\[3ex] D.\;\; 250^\circ \\[3ex] $
$ p + q = 250^\circ ...Given \\[3ex] \text{The interior angles are:} \\[3ex] 180 - p ...\text{sum of angles on a straight line} \\[3ex] 180 - q ...\text{sum of angles on a straight line} \\[3ex] s \\[3ex] \implies \\[3ex] \underline{\text{sum of interior angles of a triangle}} \\[3ex] s + 180 - p + 180 - q = 180 \\[3ex] s = 180 - 180 - 180 + p + q \\[3ex] s = -180 + 250 \\[3ex] s = 70^\circ $
If a ball is selected at random, what is the probability that it is black?
$ A.\;\; \dfrac{2}{13} \\[5ex] B.\;\; \dfrac{5}{11} \\[5ex] C.\;\; \dfrac{5}{13} \\[5ex] D.\;\; \dfrac{11}{13} \\[5ex] $
$ \text{sample space} = \{\text{2 red, 6 white, 5 black}\} \\[3ex] n(\text{sample space}) = 2 + 6 + 5 = 13 \\[3ex] P(black) = \dfrac{n(black)}{n(sample space)} \\[5ex] = \dfrac{5}{13} $
$ A.\;\; 4x \\[3ex] B.\;\; x \\[3ex] C.\;\; 2x \\[3ex] D.\;\; 3x \\[3ex] $
$ \text{data values }: (x + y), (2x + 3y), (2x - 2y), (3x - 3y) \\[3ex] \text{sum of data values} = (x + y) + (2x + 3y) + (2x - 2y) + (3x - 2y) \\[3ex] = x + y + 2x + 3y + 2x - 2y + 3x - 2y \\[3ex] = 8x \\[3ex] \text{number of data values} = 4 \\[3ex] Mean = \dfrac{\text{sum of data values}}{\text{number of data values}} = \dfrac{8x}{4} \\[5ex] = 2x $
What fraction of the work can both do together in a day?
$ A.\;\; \dfrac{1}{3} \\[5ex] B.\;\; \dfrac{1}{8} \\[5ex] C.\;\; \dfrac{2}{3} \\[5ex] D.\;\; \dfrac{1}{2} \\[5ex] $
Let the piece of work = x
Abudu can do a piece of work in 6 days
How much of that piece of work can he do in 1 day?
$ x \hspace{3em}\rightarrow\hspace{3em} 6\;\;days \\[3ex] \dfrac{x}{6} \hspace{3em}\leftarrow\hspace{3em} 1\;\;day \\[3ex] $ Efah can do the same piece of work in 3 days
How much of that piece of work can he do in 1 day?
$ x \hspace{3em}\rightarrow\hspace{3em} 3\;\;days \\[3ex] \dfrac{x}{3} \hspace{3em}\leftarrow\hspace{3em} 1\;\;day \\[3ex] $ What fraction of the work can both do together in a day?
$ \dfrac{x}{6} + \dfrac{x}{3} \\[5ex] = \dfrac{3x + 6x}{18} \\[5ex] = \dfrac{9x}{18} \\[5ex] = \dfrac{x}{2} \\[5ex] = \dfrac{1}{2}x \\[5ex] $ At the same rate, the fraction of the piece of work that both Abudu and Efah can do is $\dfrac{1}{2}$
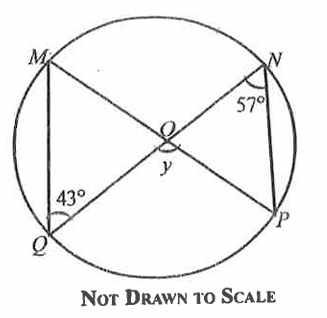
In the diagram, MNPQ is a circle, centre O.
$\angle MQN = 43^\circ$ and $\angle QNP = 57^\circ$.
Find the value of y
$ A.\;\; 70^\circ \\[3ex] B.\;\; 90^\circ \\[3ex] C.\;\; 80^\circ \\[3ex] D.\;\; 100^\circ \\[3ex] $
$ \angle QMO = 57^\circ ...\text{angles in the same segment are congruent} \\[3ex] y = \angle MQO + \angle QMO ...\text{exterior angle of a triangle = sum of interior opposite angles} \\[3ex] y = 43 + 57 \\[3ex] y = 100^\circ $
$ A.\;\; \{x: 2 \le x \lt 6\} \\[3ex] B.\;\; \{x: 2 \le x \le 6\} \\[3ex] C.\;\; \{x: 2 \lt x \le 6\} \\[3ex] D.\;\; \{x: 2 \lt x \lt 6\} \\[3ex] $
$ P = \{x: 1 \le x \le 6\} \\[3ex] Q = \{x: 2 \lt x \lt 9\} \\[5ex] \underline{\text{Lower Bound}} \\[3ex] 2 \lt \; \text{because it is contained inside } 1 \le \\[5ex] \underline{\text{Upper Bound}} \\[3ex] \le 6 \; \text{because it is contained inside } \lt 9 \\[5ex] \therefore P \cap Q = \{x: 2 \lt x \le 6\} \\[3ex] $ Student: I do not understand what you did.
Can you elaborate?
Teacher: Okay, let's explain it this way.
Let's assume that $x \in Z$ (set of integers, $Z$ rather than the set of real numbers, $R$)
This assumption is okay for this example because the set of integers is a subset of the set of real numbers.
$ P = \{1, 2, 3, 4, 5, 6\} \\[3ex] Q = \{3, 4,5 , 6, 7, 8\} \\[3ex] P \cap Q = \{3, 4, 5, 6\} \\[3ex] = \{x: 2 \lt x \le 6\}...\text{based on the options} $
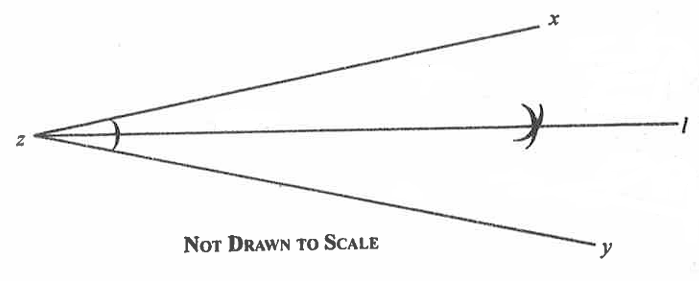
A. Locus of points equidistant from x and z
B. Locus of points equidistant from x and y
C. Locus of points equidistant from xy and zy
D. Locus of points equidistant from zx and zy
The diagram did not indicate the angle bisector of $\angle xzy$
We shall assume such because if $\angle xzy$ was not bisected (unequally divided in two parts), then none of the options would apply.
Let us analyze each option:
A. Locus of points equidistant from x and z
This is the perpendicular bisector of line segment xz
Incorrect option.
B. Locus of points equidistant from x and y
This is the perpendicular bisector of line segment xy
Incorrect option.
C. Locus of points equidistant from xy and zy
The sides do not form $\angle xzy$.
Incorrect option.
D. Locus of points equidistant from zx and zy
Angle Bisector Theorem: Any point on the bisector of an angle is equidistant from the two sides of the angle.
The straight line segment, $\overline{zl}$ that divides $\angle xzy$ is the angle bisector of the angle.
The locus of points that lie on this angle bisector consists of all points that are equidistant from the two arms of the angle, which are the line segments $\overline{zx}$ and $\overline{zy}$
The correct option is D.
$ A.\;\; 5 \\[3ex] B.\;\; 3 \\[3ex] C.\;\; 4 \\[3ex] D.\;\; 2 \\[3ex] $
$ p^2 + q^2 + r^2 = 50 \\[3ex] p = 5 \\[3ex] \sqrt{q} = 2 \implies q = 2^2 = 4 \\[3ex] 5^2 + 4^2 + r^2 = 50 \\[3ex] 25 + 16 + r^2 = 50 \\[3ex] r^2 = 50 - 25 - 16 \\[3ex] r^2 = 9 \\[3ex] r = \pm \sqrt{9} \\[3ex] r = \pm 3 \\[3ex] $ The positive value of $r = 3$
Calculate, correct to two decimal places, its volume. $\left[Take\;\;\pi = \dfrac{22}{7}\right]$
$ A.\;\; 553.14\;cm^3 \\[3ex] B.\;\; 640.87\;cm^3 \\[3ex] C.\;\; 838.67\;cm^3 \\[3ex] D.\;\; 770.32\;cm^3 \\[3ex] $
$ \underline{\text{For a Cone}} \\[3ex] V = \dfrac{\pi r^2 h}{3} \\[3ex] where \\[3ex] V = volume \\[3ex] r = radius = 8\;cm \\[3ex] l = \text{slant height} = 14\;cm \\[3ex] h = ? \\[3ex] \text{We need to find the height} \\[3ex] l^2 = r^2 + h^2 \\[3ex] h^2 = l^2 - r^2 \\[3ex] h^2 = 14^2 - 8^2 \\[3ex] = 196 - 64 \\[3ex] = 132 \\[3ex] h = \sqrt{132} \\[3ex] h = 11.48912529 \\[5ex] V = \dfrac{1}{3} * \dfrac{22}{7} * 8^2 * 11.48912529 \\[5ex] = \dfrac{1 * 22 * 64 * 11.48912529}{3 * 7} \\[5ex] = 770.3184958 \\[3ex] \approx 770.32\;cm^3 $
$ A.\;\; p = 2, \; q = -5, \; r = 3 \\[3ex] B.\;\; p = 2, \; q = 5, \; r = 3 \\[3ex] C.\;\; p = 2, \; q = 5, \; r = -3 \\[3ex] D.\;\; p = -2, \; q = 5, \; r = 3 \\[3ex] $
$ Given:\;\;px^2 + qx + r = 0 \\[3ex] Compare:\;\;ax^2 + bx + c = 0 \\[3ex] a = p \\[3ex] b = q \\[3ex] c = r \\[5ex] roots = \dfrac{1}{2} \hspace{1em}and\hspace{1em} -3 \\[5ex] \text{Sum of roots} = -\dfrac{b}{a} = -\dfrac{q}{p} \\[5ex] \text{Sum of roots} = \dfrac{1}{2} + -3 \\[5ex] = \dfrac{1}{2} - 3 \\[5ex] = \dfrac{1 - 6}{2} \\[5ex] = -\dfrac{5}{2} \\[5ex] \implies \\[3ex] -\dfrac{q}{p} = -\dfrac{5}{2} \\[5ex] \dfrac{q}{p} = \dfrac{5}{2} \\[5ex] q = 5 \\[3ex] p = 2 \\[5ex] \text{Product of roots} = \dfrac{c}{a} = \dfrac{r}{p} \\[5ex] \text{Product of roots} = \dfrac{1}{2} * -3 = -\dfrac{3}{2} \\[5ex] \implies \\[3ex] \dfrac{r}{p} = -\dfrac{3}{2} \\[5ex] p = 2 ...\text{confirming from previous} \\[3ex] r = -3 \\[5ex] p = 2, \; q = 5, \; r = -3 $
$ A.\;\; N\;50^\circ\;W \\[4ex] B.\;\; N\;40^\circ\;W \\[4ex] C.\;\; N\;50^\circ\;E \\[4ex] D.\;\; N\;40^\circ\;E \\[4ex] $
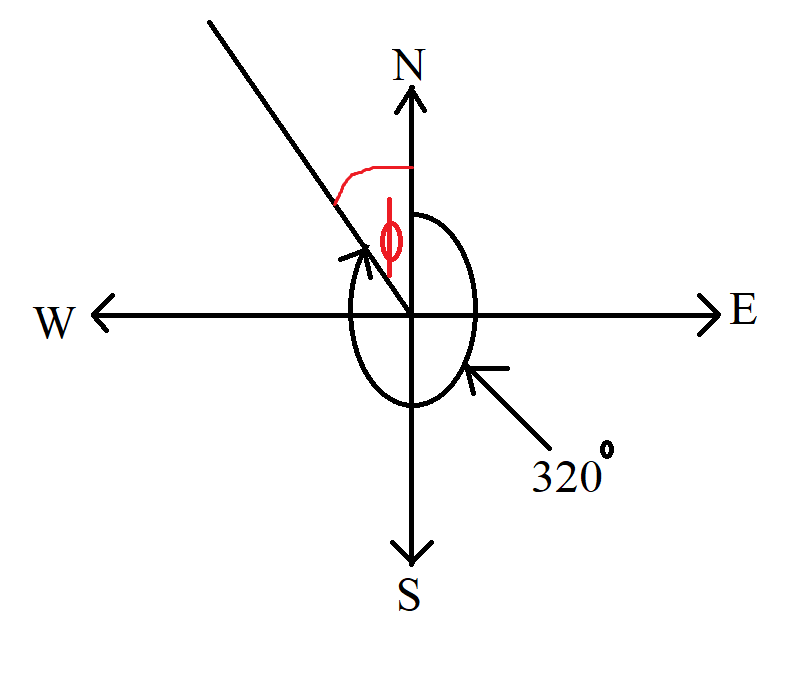
$ 320 + \phi = 360 ...\angle s\;\;at\;\;a\;\;point \\[3ex] \phi = 360 - 320 \\[3ex] \phi = 40^\circ \\[3ex] Compass\;\;Bearing = N\;40^\circ\;W $


