Set Theory
Welcome to Our Site
I greet you this day,
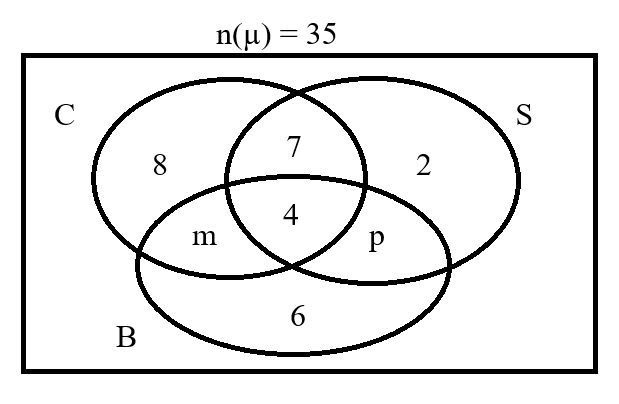
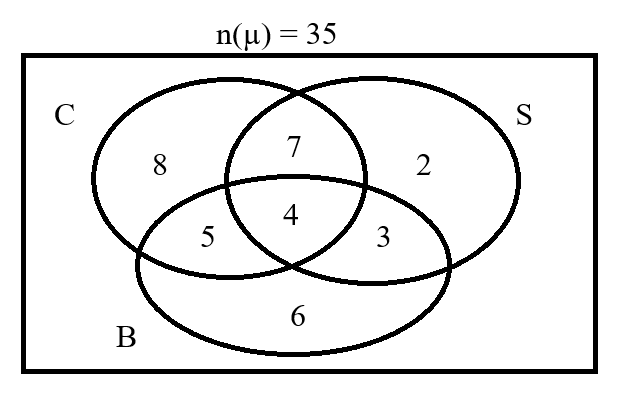
These are the solutions to the WASSCE past questions on the topic: Sets.
When applicable, the TI-84 Plus CE calculator (also applicable to TI-84 Plus calculator) solutions are provided
for some questions.
The link to the video solutions will be provided for you. Please
subscribe to the YouTube channel to be notified of upcoming livestreams. You are welcome to ask questions during
the video livestreams.
If you find these resources valuable and helpful in your passing the
Mathematics exam of WASSCE, please consider making a donation:
Cash App: $ExamsSuccess or
cash.app/ExamsSuccess
PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess
Google charges me for the hosting of this website and my other
educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well.
As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.
Comments, ideas, areas of improvement, questions, and constructive
criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.
Out of the number, 24 preferred Cymbal, 16 Saxophone and 18 Bongo.
8 preferred Cymbal only, 2 Saxophone only and 6 Bongo only.
4 played all the three instruments while 7 preferred Cymbal and Saxophone only.
(a.) Illustrate the information in a Venn diagram.
(b.) Find the number of artistes who preferred:
(i.) only two types of instruments;
(ii.) only one type of instrument.
Let:
Cymbal = C
Saxophone = S
Bongo = B
universal set = μ
$ n(\mu) = 35 \\[3ex] n(C) = 24 \\[3ex] n(S) = 16 \\[3ex] n(B) = 18 \\[3ex] n(\text{only C}) = 8 \\[3ex] n(\text{only S}) = 2 \\[3ex] n(\text{only B}) = 6 \\[3ex] n(\text{C and S and B}) = 4 \\[3ex] n(\text{only C and S}) = 7 \\[3ex] n(\text{only C and B}) = m \\[3ex] n(\text{only S and B}) = p \\[3ex] $ The Venn diagram based on the information is:
$ 8 + 7 + 4 + m = n(C) \\[3ex] 19 + m = 24 \\[3ex] m = 24 - 19 \\[3ex] m = 5 \\[5ex] 7 + 2 + 4 + p = n(S) \\[3ex] 13 + p = 16 \\[3ex] p = 16 - 13 \\[3ex] p = 3 \\[5ex] 8 + 7 + 4 + 5 + 2 + 3 + 6 = 35 \\[3ex] n(\text{neither of C, S, and B}) = 35 - 35 = 0 \\[3ex] $ (a.) The updated Venn diagram is:
$ (b.)(i.) \\[3ex] n(\text{only two types of instruments}) \\[3ex] = n(\text{only C and S}) + n(\text{only C and B}) + n(\text{only S and B}) \\[3ex] = 7 + 5 + 3 \\[3ex] = 15\;artistes \\[5ex] (ii.) \\[3ex] n(\text{only one type of instrument}) \\[3ex] = n(\text{only C}) + n(\text{only S}) + n(\text{only B}) \\[3ex] = 8 + 2 + 6 \\[3ex] = 16\;artistes $
